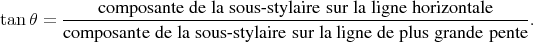Tableaux récapitulatifs et réflexion complémentaire

7 Tableaux récapitulatifs et réflexion complémentaire

Nous résumons dans les tableaux 1, 2 et 3 les différents cas étudiés.

	Horizontal	Horizontal incliné (i)


Hyperbole	cos ²δ_s - sin ²φ > 0	cos ²δ_s - sin ²(φ - i) > 0

Parabole	cos ²δ_s - sin ²φ = 0	cos ²δ_s - sin ²(φ - i) = 0

Ellipse	cos ²δ_s - sin ²φ < 0	cos ²δ_s - sin ²(φ - i) < 0

Cercle	φ = ±π∕2	i = φ - π∕2

Droite	δ_s = 0	δ_s = 0

TAB. 1:

Lignes de déclinaison d’un cadran horizontal et horizontal incliné.

	Vertical	Vertical déclinant (Δ)


Hyperbole	cos ²δ_s - cos ²φ > 0	cos ²δ_s - cos ²φ cos ²Δ > 0

Parabole	cos ²δ_s - cos ²φ = 0	cos ²δ_s - cos ²φ cos ²Δ = 0

Ellipse	cos ²δ_s - cos ²φ < 0	cos ²δ_s - cos ²φ cos ²Δ < 0

Cercle	φ = 0	φ = 0, Δ = 0(+π)

Droite	δ_s = 0	δ_s = 0

TAB. 2:

Lignes de déclinaison d’un cadran vertical et vertical déclinant.

	Déclinant incliné


Hyperbole	ζ² + cos ²φ sin ²Δ - sin ²δ_s > 0

Parabole	ζ² + cos ²φ sin ²Δ - sin ²δ_s = 0

Ellipse	ζ² + cos ²φ sin ²Δ - sin ²δ_s < 0

Cercle	Δ = 0, i = φ - π∕2

Droite	δ_s = 0

TAB. 3:

Lignes de déclinaison d’un cadran déclinant incliné, avec ζ = cos φ cos Δ cos i + sin φ sin i.

Une étude attentive des tableaux 1 à 3 montre qu’il est relativement aisé de déterminer toutes les conditions à partir du seul cas du cadran vertical en effectuant des transformations minimes.

Ainsi, on s’aperçoit dans la table 2 qu’il suffit de convertir cos φ en cos φ cos Δ pour passer du cadran vertical au cadran vertical déclinant. Ce terme n’est autre que la valeur ._D obtenue à partir des équations (16) ou (19), c’est-à-dire la composante hors plan de la table du vecteur directeur du style, soit encore (en multipliant par L_s) la mesure algébrique du style droit. On peut donc effectuer la même opération avec l’équation (41), et il faut alors substituer cos Δ sin i cos φ - cos i sin φ à cos φ pour obtenir les relations de la table 3 (on vérifie aisément que cos ²δ_s - (cos Δ sin i cos φ - cos i sin φ)² = ζ² + cos ²φ sin ²Δ - sin ²δ_s).

De même, l’angle dont il faut tourner le système d’axe pour s’affranchir des termes croisés y_DIz_DI dans les équations des lignes de déclinaison s’obtient facilement avec la relation

⃗ ′ tanθ = - OB--.⃗yDI-, O⃗B ′.⃗zDI

(49)

ce n’est autre que l’angle entre la sous-stylaire et la ligne de plus grande pente (confondue avec la ligne de midi sauf dans le cas du cadran déclinant incliné).

Pour résumer, on peut dire que :

dans tous les cas, la nature de la ligne de déclinaison est donnée par le signe du terme test cos ²δ_s - (._DI)², c’est-à-dire par la comparaison de la longueur L_s cos δ_s avec la mesure algébrique du style droit HB′ = ._DI,
l’angle de rotation θ permettant d’éliminer les termes croisés y_DIz_DI est tel que
$composante de la sous-stylaire sur la ligne horizontale tan θ = -----------------------------------------------------------. composante de la sous-stylaire sur la ligne de plus grande pente$ (50)

Cette rotation correspond dans tous les cas à rendre l’axe (Oy′) parallèle à la droite des équinoxes, et par conséquent, à le rendre perpendiculaire à la sous-stylaire.

[next] [prev] [prev-tail] [front] [up]