Cadran déclinant incliné

6 Cadran déclinant incliné

On part toujours du cadran vertical méridional déclinant, et on l’incline (conformément à [3]), ce qui conduit à prendre pour système de coordonnées le repère (0,_DI,_DI,_DI) avec _DI la ligne de plus grande pente ascendante (figure 7). On peut montrer que les coordonnées du vecteur ⃗ ′
OB dans ce nouveau repère sont alors

( ) cosΔ sinicos φ - cosisin φ OB⃗ ′DI = (Py)-1.(Pz)-1.O⃗B ′ = Ls ( sin Δ cosφ ) - sin isin φ - cos Δ cosicos φ

(41)

(les matrices de changement de base utilisées sont détaillées dans l’annexe B).

FIG. 7:

Cadran déclinant incliné (d’après la figure 16b de [3]).

Le point B′ doit avoir sa coordonnée x positive dans le nouveau repère, sinon il n’est pas du coté de la face visible du cadran. Si cette composante est négative, alors il faut retourner le style, ce qui revient tout simplement à transformer O⃗B ′ en -. Pour cette raison on définit A = cos Δ sin i cos φ- cos i sin φ et on introduit κ tel que κ = 1 si A > 0 et κ = -1 si A < 0 (encore une fois, la notation est identique à celle de [3]). En multipliant ′
O⃗B par κ, on est sûr de toujours avoir un style droit de mesure algébrique HB′ = κ O⃗B ′ ._DI positive et donc le style sur la bonne face du cadran.

L’équation générale obtenue est

y2 (cos2 φsin2Δ - sin2δ ) + z2 (ζ2 - sin2 δ) DI s2 DI 2s + - 2κyDI Lscos φ sin Δ cos δs + 2κzDI Lsζ cos δs - 2yDI zDIζ cosφ sin Δ + L2 cos2δs s = 0, (42 )

avec

ζ = cosφ cosΔ cos i + sin φsini.

(43)

Pour δ_s = 0, on obtient l’équation

κ(yDI cosφ sinΔ - zDIζ) = Ls,

(44)

donc l’ombre parcourt la droite définie par

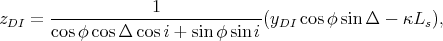------------1-------------- zDI = cosφ cosΔ cosi + sin φsini(yDI cosφ sinΔ - κLs ),

(45)

qui est bien le résultat trouvé dans la référence [3] (avec κ = 1).

Comme pour le cas du cadran vertical déclinant de la section 5, on peut trouver un système de coordonnées permettant de s’affranchir du terme croisé dans l’équation (42). L’angle de rotation est donné par la relation

tan θ = --------cosφ-sinΔ----------= --------sinΔ----------, cosφ cosΔ cosi + sin φsin i cosΔ cos i + tan φ sin i

(46)

ce qui est en accord avec la pente de la droite définie par l’équation (45) : cet angle θ correspond donc à l’angle que fait la ligne des équinoxes avec l’axe horizontal (Oy_DI), ainsi qu’à l’angle (noté ω dans [3]) que fait la sous-stylaire O⃗H avec la ligne de plus grande pente (Oz_DI).

Dans le nouveau système de coordonées, on peut écrire l’équation de la trajectoire de l’ombre sous la forme a′y′² + c′z′² + d′y′ + f′z′ + g′ = 0, avec

a′ = - sin2 δs, (47a ) ′ 2 2 2 2 c = ζ + cos φ sin Δ - sin δs, (47b ) d′ = 0, (47c ) ∘ ----------------- f ′ = κLs cos2δs ζ2 + cos2φ sin2Δ, (47d ) ′ 2 2 g = Ls cos δs (47e )

(on peut vérifier que pour i = π∕2, on retrouve bien le résultat du cadran vertical méridional).

Ceci est une hyperbole si a′ et c′ sont de signe opposé, donc si

2 2 2 2 ζ + cos φ sin Δ - sin δs > 0.

(48)

[next] [prev] [prev-tail] [front] [up]