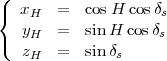
La Terre tourne autour du Soleil, mais bien sûr vu de la Terre, on dirait plutôt que c’est le Soleil qui tourne autour de la Terre. Pour cette raison, on cherche à exprimer la position du Soleil par rapport à un repère local.
Dans le repère équatorial absolu, la position du Soleil est repérée par l’ascension droite et la déclinaison, qui correspondent respectivement à l’angle que fait la projection du Soleil sur l’équateur céleste avec le point vernal, et à l’angle entre le Soleil et l’équateur céleste. L’ascension droite s’exprime en heures, minutes et secondes, alors que la déclinaison s’exprime en degrés.
On rappelle que l’inclinaison de l’axe de la Terre par rapport au plan de l’écliptique (obliquité) est ε = 23°27′ = 23,45° et que la déclinaison δs vérifie -ε < δs < ε.
Dans le repère équatorial local ayant pour plan de référence le plan de l’équateur céleste et pour grand cercle origine le méridien local, la déclinaison du Soleil est la même que dans le repère équatorial absolu [2], mais la longitude du Soleil sera comptée à partir du méridien local. Elle sera appelée «angle horaire» et notée H (figure 1(a) ). La position du Soleil s’écrit donc en fonction de H :
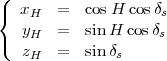
|
(1) |
|
Dans le repère local horizontal ayant pour plan de référence le plan de l’horizon local et pour grand cercle origine le méridien local, la position du Soleil telle qu’elle est perçue par un observateur situé à la latitude φ et à la longitude λL est repérée par les angles appelés azimut et élévation (ou hauteur), respectivement notés A et h (figure 1(b)). On a donc :
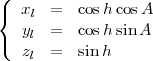
|
(2) |
Le plan horizontal local étant incliné de -(π∕2 - φ) par rapport au plan équatorial, on obtient à l’aide d’une matrice de rotation (voir l’annexe A ) une autre écriture de la position du Soleil :
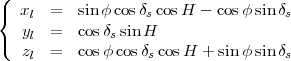
|
(3) |
et donc en combinant les équations (2 ) et (3) on obtient finalement :
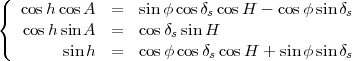
|
(4) |
À midi vrai (H = 0, A = 0), on obtient
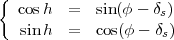
|
(5) |