|
|
Un cadran solaire horizontal comporte un style incliné de π∕2 - φ par rapport à la verticale locale de sorte à ce qu’il soit parallèle à l’axe de rotation de la Terre. Il pointe donc en direction du Nord.
|
|
On va cependant étudier dans un premier temps le cas du style vertical, qui permet d’établir quelques relations utiles par la suite.
Pour l’angle horaire H , la longueur L′ = ||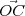
||
de l’ombre au sol d’un style vertical de longueur
L = ||
||
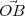vérifie la relation (figure 2
) :
|
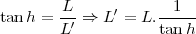
(6) |
L’angle A que fait l’ombre avec le méridien local (l’azimut, donc) vérifie (facilement obtenu à partir de l’équation (4 ))
|
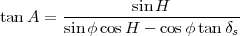
(7) |
Cet angle dépend de H et φ bien sûr, mais également de δs.
La longueur L′p de la projection de l’ombre du style sur le méridien local vaut
|
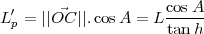
(8) |
Or lorsque δs = 0 (équinoxes de printemps et d’automne), on a (d’après (4 ))
|
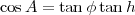
(9) |
donc dans ce cas particulier, la longueur de la projection est une constante :
|
(10) |
L’extrémité de l’ombre parcourt donc une droite perpendiculaire au méridien local.
On incline le style de manière
à ce qu’il fasse un angle π∕2 -
φ avec la verticale. Il
est alors parallèle à l’axe de rotation de la
Terre. On note Ls
= ||
|| la longueur du style incliné,
définie par la relation
|
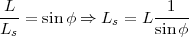
(11) |
Dans le triangle (OO′C′), on a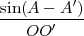 
= 
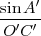. Après un peu de calcul, on trouve la
relation
|
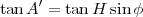
(12) |
Dans le cas du style incliné, l’angle que fait l’ombre avec le méridien local en fonction de H ne dépend plus de la déclinaison δs, d’où l’intérêt de cette géométrie pour la construction d’un cadran solaire. La longueur L′s = OC′ de l’ombre peut se calculer assez facilement :
|
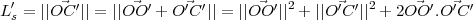
(13) |
On trouve finalement puisque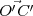 
= 
:
|
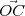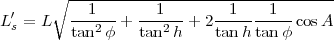
(14) |
À midi vrai, la relation (14) se simplifie et la longueur de l’ombre devient
|
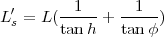
(15) |
En utilisant les relations (5) et (11), on peut encore simplifier pour obtenir une relation entre la longueur de l’ombre et la longueur du style incliné à midi vrai :
|
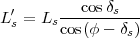
(16) |
Si l’on regarde la longueur L′sp de la projection de l’ombre sur le méridien local, on a cette fois
|
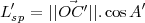
(17) |
Pour le cas particulier δs = 0, on obtient après calcul la relation
|
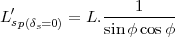
(18) |
L′
sp(δs=0) est donc une
constante et l’extrémité de l’ombre
parcourt une droite perpendiculaire au méridien local. En
fait cette propriété est évidente
après le calcul du style droit et l’étude
attentive de la figure 2
, la valeur de la
projection pouvant être calculée également
très facilement si l’on appelle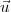 
le vecteur
unitaire porté par le méridien local et
dirigé vers le Nord :
|
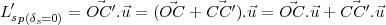
(19) |
or le calcul de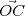 
.
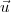correspond à celui du style droit,
et par construction 
= 
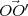, on en déduit donc
finalement
|
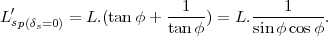
(20) |
On peut constater que l’équation (20 ) est identique à (18 ) et est bien compatible avec l’équation (16 ).
Avec les formules qui précèdent, on est en mesure de dessiner un cadran solaire. Le cadran représenté sur la figure 3 a été calculé pour une latitude de 48,3° Nord. Les points notés O et O′ correspondent aux points du même nom sur la figure 2 .
La courbe en huit visible sur la ligne du midi vrai est parfois appelée analemme. Elle est la conséquence de l’équation du temps. Les lignes de déclinaison pour les solstices et les équinoxes sont également visibles, et ont été ici calculées à partir de la formule (14).
En première approximation, on peut considérer que le Soleil se lève et se couche lorsque h = 0 (dans la pratique, il faut tenir compte du diamètre angulaire du Soleil et de la réfraction de l’atmosphère). Des équations (4 ), on déduit qu’à ce moment là, H doit vérifier la relation
|
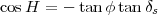
(21) |
On montre qu’alors
|
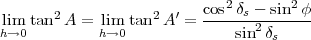
(22) |
Lorsque le Soleil se couche, son ombre suit donc une asymptote dont la pente est donnée par (22 ).
Il est cependant possible que le Soleil ne se lève jamais ou ne se couche jamais. En effet, sinh > 0 implique par exemple φ > π∕2 - δ. Au Pôle Nord (φ = π∕2), cette relation est vérifiée dès que δ > 0, c’est-à-dire de l’équinoxe de printemps à l’équinoxe d’automne. De manière plus générale, pour des latitudes supérieures à 66°33′ ou inférieures à -66°33′ (latitudes des cercles polaires), il existe un ou plusieurs jours où le Soleil ne se lève pas et où le Soleil ne se couche pas (plus on se rapproche des pôles, plus cette durée est longue).
