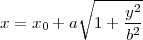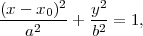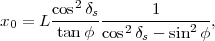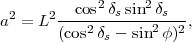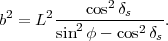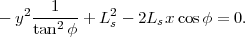4 Équations des lignes de
déclinaison
À un jour donné de
l’année correspond une valeur δs de la déclinaison. Pour une valeur
de la déclinaison, l’extrémité de
l’ombre du style suit une trajectoire bien précise.
On a déjà vu précédemment que dans le
cas particulier des équinoxes (δs = 0),
cette trajectoire était une droite.
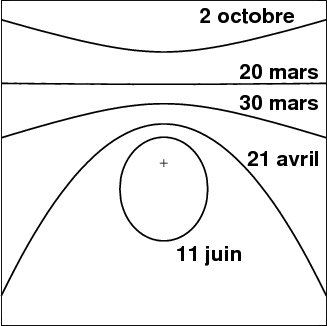
On va noter 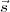 le vecteur unitaire indiquant la position
du Soleil, en choisissant comme axe
le vecteur unitaire indiquant la position
du Soleil, en choisissant comme axe 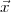 le méridien local et comme
sens positif la direction vers laquelle pointe le style, donc le
Nord. D’après le système (3
)
le méridien local et comme
sens positif la direction vers laquelle pointe le style, donc le
Nord. D’après le système (3
) 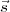 a pour composantes dans ce nouveau
repère
a pour composantes dans ce nouveau
repère

|
(23) |
Le vecteur 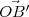 représentant le style
s’écrit quant à lui
représentant le style
s’écrit quant à lui

|
(24) |
Le produit scalaire de ces deux vecteurs
donne
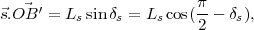
|
(25) |
il s’agit donc d’une constante (pour
un jour donné) ! De cette dernière
relation, on peut conclure que pour une déclinaison
fixée, la surface balayée par le rayon vecteur
 au cours
d’une journée définit un cône de
révolution dont l’axe est le style incliné
(en réalité, il s’agit plutôt de
l’axe de rotation de la Terre, mais vu du Soleil, on peut
considérer qu’ils sont confondus), dont le sommet
est l’extrémité B′ du style, et dont le demi-angle
d’ouverture au sommet vaut π∕2 -
δs (figure 4
). Cet angle peut être
facilement visualisé sur la figure 1(a)
en se souvenant que le style
OB′ est parallèle à
l’axe des pôles.
au cours
d’une journée définit un cône de
révolution dont l’axe est le style incliné
(en réalité, il s’agit plutôt de
l’axe de rotation de la Terre, mais vu du Soleil, on peut
considérer qu’ils sont confondus), dont le sommet
est l’extrémité B′ du style, et dont le demi-angle
d’ouverture au sommet vaut π∕2 -
δs (figure 4
). Cet angle peut être
facilement visualisé sur la figure 1(a)
en se souvenant que le style
OB′ est parallèle à
l’axe des pôles.
Les lignes de déclinaison vont ainsi
être définies comme l’intersection du
cône précédemment défini et du plan
horizontal du cadran solaire. D’un point de vue purement
mathématique, cette intersection peut être un
cercle, une ellipse, une parabole ou une hyperbole.
Par construction, si l’on
considère un point M
de la ligne de déclinaison (ses coordonnées sont
(x,y,0)), alors 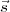 et
et 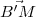 sont colinéaires
(M est la projection de
B′ dans le plan suivant la direction
du Soleil
sont colinéaires
(M est la projection de
B′ dans le plan suivant la direction
du Soleil 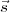 , autrement dit l’ombre du sommet B′ du style). On en déduit
donc
, autrement dit l’ombre du sommet B′ du style). On en déduit
donc
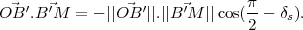
|
(26) |
Sachant que
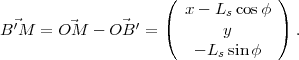
|
(27) |
après élévation au
carré on trouve
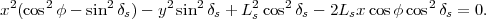
|
(28) |
Après mise en forme et en profitant du
fait que cos2φ
- sin2δs =
cos2δs -
sin2φ,
on obtient finalement
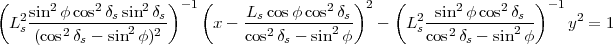
|
(29) |
4.1
Lignes de
déclinaison si le Soleil se couche
Pour des latitudes où le Soleil se
couche tous les jours de l’année, on a cos2δs -
sin2φ
> 0, et on peut
alors simplifier l’équation (29) en
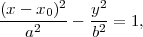
|
(30) |
avec
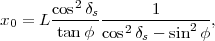
|
(31) |
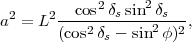
|
(32) |
et

|
(33) |
L’équation (30)
représente une hyperbole (voir figure 5). Ses
asymptotes sont
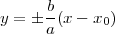
|
(34) |
et elles se croisent au point (x0,0).
On peut vérifier qu’on a bien, conformément
à l’équation (22
) :
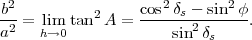
|
(35) |
Les points de coordonnées (x0
± a,0)
(situés sur la courbe) sont nommés vertex.
Il est surprenant de constater que x0
est la longueur moyenne de l’ombre à midi vrai pour
les déclinaisons δs et -δs. En effet,
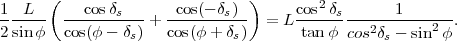
|
(36) |
On peut remarquer de façon plus
générale que x0
et les pentes ±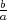 des asymptotes sont invariantes
par la transformation δs →-δs. Les lignes de déclinaison
δs et -δs correspondent donc aux deux branches de
la même hyperbole.
des asymptotes sont invariantes
par la transformation δs →-δs. Les lignes de déclinaison
δs et -δs correspondent donc aux deux branches de
la même hyperbole.
On peut tracer les lignes de déclinaison
grâce à la formule
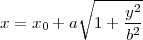
|
(37) |
Pour δs = 0,
on obtient a = 0, et donc
l’équation (37
) se réduit
à x = x0,
ce qui est bien une droite. Par ailleurs on vérifie bien
que x0 =
L∕(sinφcosφ), ce qui est conforme à
l’équation (18
).
4.2
Lignes de
déclinaison si le Soleil ne se couche pas
Si l’on se trouve à une latitude
où le Soleil ne se couche pas un jour de
déclinaison δs, alors cos2δs -
sin2φ
< 0, et
l’équation (29
) est alors celle d’une
ellipse :
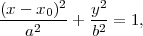
|
(38) |
avec
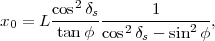
|
(39) |
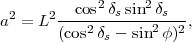
|
(40) |
et
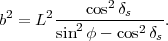
|
(41) |
La transition entre la période où
le Soleil se couche et la période où il ne se
couche pas se fait lorsque cos2δs -
sin2φ
= 0, c’est-à-dire
le jour où δs =
π∕2 -
φ dans
l’hémisphère nord et δs =
-π∕2 -
φ dans
l’hémisphère sud. Dans ce cas,
l’équation (29
) n’est pas utilisable
(le dénominateur des différents termes est nul) et
il faut alors revenir à
l’équation (28
), qui se simplifie pour
donner (toujours en utilisant cos2φ
- sin2δs =
cos2δs -
sin2φ) :
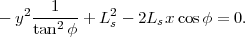
|
(42) |
La trajectoire décrite par l’ombre
de l’extrémité du style ce jour particulier
est donc une parabole.
4.3
Exemples de lignes de
déclinaison
À l’aide des
équations (30
) et (38), on peut
alors calculer facilement les lignes de déclinaison pour
une latitude fixée. Nous avons choisi une latitude de
78°, pour laquelle il
arrive que le Soleil ne se couche pas (et donc ne se lève
pas également). Le résultat est
présenté sur la figure 6
. Les lignes ont
été calculées pour les 20 mars, 30 mars, 21
avril, 11 juin et 2 octobre. Le point de contact entre le style
et le plan horizontal est symbolisé par une croix.
On observe quatre types de courbes : l’hyperbole, les 30 mars et 2
octobre, la ligne droite pour l’équinoxe,
l’ellipse le 11 juin, et la parabole le 21 avril puisque ce
jour là on a δs =
90°- φ =
12°.
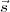 le vecteur unitaire indiquant la position
du Soleil, en choisissant comme axe
le vecteur unitaire indiquant la position
du Soleil, en choisissant comme axe 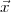 le méridien local et comme
sens positif la direction vers laquelle pointe le style, donc le
Nord. D’après le système (3
)
le méridien local et comme
sens positif la direction vers laquelle pointe le style, donc le
Nord. D’après le système (3
) 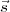 a pour composantes dans ce nouveau
repère
a pour composantes dans ce nouveau
repère
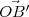 représentant le style
s’écrit quant à lui
représentant le style
s’écrit quant à lui
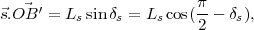
 au cours
d’une journée définit un cône de
révolution dont l’axe est le style incliné
(en réalité, il s’agit plutôt de
l’axe de rotation de la Terre, mais vu du Soleil, on peut
considérer qu’ils sont confondus), dont le sommet
est l’extrémité
au cours
d’une journée définit un cône de
révolution dont l’axe est le style incliné
(en réalité, il s’agit plutôt de
l’axe de rotation de la Terre, mais vu du Soleil, on peut
considérer qu’ils sont confondus), dont le sommet
est l’extrémité 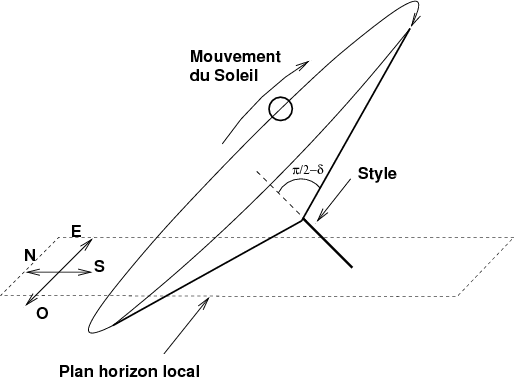
 au cours d’une
journée.
au cours d’une
journée.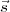 et
et 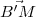 sont colinéaires
(
sont colinéaires
(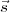 , autrement dit l’ombre du sommet
, autrement dit l’ombre du sommet 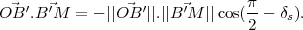
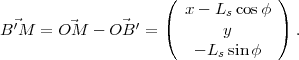
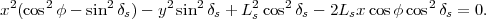
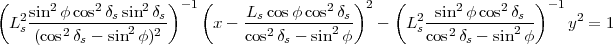
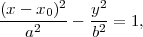
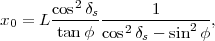
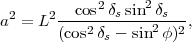

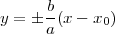
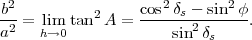

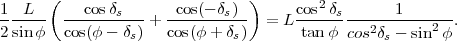
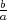 des asymptotes sont invariantes
par la transformation
des asymptotes sont invariantes
par la transformation