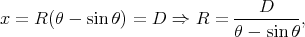
Après avoir résolu l’énigme de son frère, Jacques Bernoulli lui soumit en retour le problème suivant, variation du premier : quelle la trajectoire permettant d’aller le plus rapidement d’un point à une ligne verticale. Il s’agit bien sûr d’un arc de cycloïde, mais parmi toutes les cycloïdes passant par le point d’origine et un point de la droite, laquelle est-ce ? On peut encore une fois résoudre ce problème à l’aide des variations ou à l’aide d’une méthode plus géométrique [4], mais nous allons résoudre ce problème à l’aide d’une simple dérivation.
On fixe la distance D de la droite verticale à l’origine, par conséquent on peut exprimer R en fonction de D et θ
|
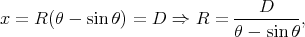| (16) |
et on peut exprimer le temps de parcours uniquement en fonction de θ
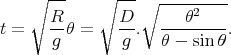 | (17) |
On peut alors étudier la variation de t en fonction de θ, ou encore plus simplement celle de t2
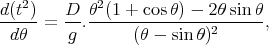 | (18) |
et on vérifie que
 | (19) |
donc la cycloïde cherchée a pour paramètres θ = π et R =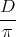 
, et la trajectoire au point d’arrivée sur la
droite est perpendiculaire à cette dernière. On peut montrer de manière générale que la brachistochrone
coupe à angle droit la courbe d’arrivée [5] quelle qu’elle soit, et pour des points de départ d’arrivée se
trouvant sur deux courbes distinctes, le trajet donnant le temps de parcours le plus court entre ces deux
courbes est comme déjà indiqué perpendiculaire à la courbe d’arrivée, mais en plus les tangentes aux
courbes aux points de départ et d’arrivée sont parallèles entre elles [6]. Cette propriété est illustrée par la
figure 2.
|
|
Dans la pratique, l’expérience n’est pas réalisée avec un point matériel pesant qui glisse sans frottement,
mais avec une bille qui roule. Il faut donc en tenir compte dans la définition de l’énergie cinétique, qui
inclut un terme dépendant du moment d’inertie de la bille [3, 7]. Pour une sphère, J = 
mr2,
par conséquent Ec = 
(m + 
m)v2 = 
.
mv2. Reprenant l’équation (12), on en conclut
que
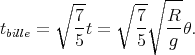 | (20) |
Il faut également bien voir que ce temps correspond à celui que mettrait le centre de masse de la bille parcourant la cycloïde. Or celui-ci parcourt une courbe « parallèle » à la cycloïde, mais qui n’est pas une cycloïde [7]. Par conséquent, il faut tenir compte de cette trajectoire modifiée pour calculer le vrai temps de parcours théorique tenant compte du rayon de la bille (ou alors modifier la trajectoire de manière à ce que ce soit bien le centre de la sphère qui parcourt la cycloïde initiale).
