Étude théorique

2 Étude théorique

2.1 Analogie avec l’optique

On sait que la lumière va d’un point à un autre par le chemin le plus rapide (principe de Fermat). Lors du passage d’un milieu d’indice n₁ à un milieu d’indice n₂, on a n₁ sin u₁ = n₂ sin u₂, or la vitesse de la lumière valant c∕n, on en déduit

sinu- -1--- v = C = v . max

(1)

Par ailleurs, la conservation de l’énergie implique

1- 2 ∘ ---- 2mv = mgy ⇒ v = 2gy.

(2)

Par conséquent on en déduit

sinu- ∘ --- √y--= C 2g

(3)

∘ ------- vmax = 2gymax,

(4)

donc

1 √y-- C = √--------⇒ sinu = √-----. 2gymax ymax

(5)

Un simple dessin montre que ẏ = dy
---
dx = tan(π∕2 - u) = cot u, et cot ²u = 1
---2--
sin u - 1 donc

--1---= 1 + ˙y2 = ymax-, sin2 u y

(6)

on obtient par conséquent l’équation différentielle caractéristique de la trajectoire

y (1 + y˙2) = ymax.

(7)

2.2 Solution analytique

On pose ẏ = cot θ-
2 et on trouve

x = ymax(θ - sinθ), (8) 2 ymax- y = 2 (1 - cosθ ). (9)

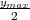Il s’agit de l’équation paramétrique d’une cycloïde dont le cercle générateur a pour rayon R = ymax
2

(figure 1).

FIGURE 1:

Trajectoire de A à B.

On peut à présent déterminer le temps de parcours du point A (θ = 0) au point B (θ = θ_B) :

∫ ∫ B B ds t = dt = --, A A v

(10)

∘ -------------------------------- ∘ ---2-----2 2 2 2 ∘ ------------ ds = dx + dy = R [(1 - 2cos θ + cos θ) + sin θ]dθ = R 2(1 - cosθ)dθ

(11)

donc avec (2) et (9) on obtient

∘ --- ∘ --- R ∫ θB R t = -- dθ = --θB. g 0 g

(12)

Remarque : autant il est facile de trouver x et y à partir de R et θ, autant l’inverse est compliqué. Le programme 2.1 permet de retrouver les paramètres R et θ à l’aide d’une méthode de minimisation incluse dans le logiciel Octave. Une autre approche basée sur l’utilisation de la méthode de Newton-Raphson peut être utilisée [3].

Exemple : on cherche la brachistochrone entre les points A(0, 0) et B(5, 2) (coordonnées exprimées en mètres). Le programme 2.1 donne comme résultats R = 1, 1244 m, θ = 3, 8197, et un temps de trajet de 1.2931 s.

Code 2.1:

Programme de détermination du rayon et de l’angle

%% Determination des parametres de la brachistochrone qui passe par
%% A et B (xA=0, yA=0)
%% calcul du temps entre A et B
%% Programme pour Octave 3.0

clear *

function obj=fun1(p)
    R=p(1);
    theta=p(2);

    xe=R*(theta-sin(theta));
    ye=R*(1-cos(theta));

    global xB yB %% valeurs definie dans le prog principal
    obj=(xB-xe)^2+(yB-ye)^2;
end

%% point d’arrivee
global xB yB

xB=input(’x final (>0) : ’)
yB=input(’y final (>0) : ’)

p0=[1;pi/2];
t=cputime();
%[p, obj, info, iter, nf, lambda]=sqp(p0,@fun1,[],[]);
[p, obj, info]=sqp(p0,@fun1,[],[])
t = cputime() - t;
printf(~Elapsed time = %f\n\n\n~,t);

Rayon=p(1)
theta=p(2)
g=9.81;
temps_trajet=sqrt(Rayon/g)*theta

tt=linspace(0,theta,100);
xx=Rayon*(tt-sin(tt));
yy=Rayon*(1-cos(tt));
plot(xx,-yy)

2.3 Solution approchée

Il est possible de trouver une solution approchée en utilisant les fonctions de minimisation fournies dans les tableurs ou les logiciels de calcul. Le principe du calcul est le suivant :

on impose un certain nombre de valeurs x_k (1 < k < N)
on cherche les valeurs y_k associées qui minimisent le temps de trajet (les valeurs y₁ et y_N sont bien évidement connues), calculé comme suit :
1. on calcule l’énergie potentielle E_p(y_k) = -mgy_k (l’axe des y est orienté positivement vers le bas),
2. on calcule l’énergie cinétique (sachant que E_c(x₁) = 0) E_c(x_k) = E_p(x₁) - E_p(x_k) = mv_k²∕2,
3. on en déduit la vitesse v_k = ,
4. on approxime ds = par Δs_k = ,
5. on calcule la vitesse moyenne sur la distance ds avec v_k^m = (v_k + v_k+1)∕2,
6. on approxime dt = ds∕v avec Δt_k = Δs_k∕v_k^m,
7. on calcule t_total = ∑ _k=1^N-1Δt_k, qui est la quantité à minimiser.

Le programme 2.2 pour Octave réalise ces différentes étapes (minimisation à l’aide de la fonction sqp).

Code 2.2:

Programme approximant la solution pour des abscisses fixées

%% Pb brachistochrone
%% Programme pour Octave 3.0

clear *

function obj=temps(h)
    m=1;
    g=9.81;

    global x hi hf
    n=length(x);

    h(1)=hi;
    h(n)=hf;

    ep=-m*g*h; % orientation des y vers le bas
    ec=zeros(1,n);
    vm=zeros(1,n);
    s=zeros(1,n);

    ec=ep(1)-ep;
    v=sqrt(2*ec/m);
    vm(2:n)=(v(1:n-1)+v(2:n))/2;
    s(2:n)=sqrt((x(2:n)-x(1:n-1)).^2+(h(2:n)-h(1:n-1)).^2);

    obj=sum(s(2:n)./vm(2:n)); % temps
end

%% CI
global x hi hf

xi=0
xf=input(’x final (>0) : ’)
hi=0
hf=input(’y final (>0) : ’)
nbpts=11
x=linspace(xi,xf,nbpts)’;

h0=linspace(hi,hf,nbpts)’;

t=cputime();
[h, obj, info]=sqp(h0,@temps,[],[])
t = cputime() - t;
printf(~Elapsed time = %f\n\n\n~,t);

plot(x,h)

On peut ensuite vérifier graphiquement que l’on retrouve un résultat proche de celui obtenu avec le programme précédent (et aussi comparer le temps estimé du trajet, ici pour des points identiques à l’exemple de la partie 2.2 on trouve t = 1, 3072 s.

2.4 Propriétés remarquables

2.4.1 Tautochronie

En partant du point d’altitude y = y₀ (le cercle générteur a tourné de θ₀), la vitesse s’exprime comme

∘ ---------- ∘ ------------------- v = 2g (y - y0) = 2gR (cos θ0 - cosθ)

(13)

donc avec dt = ds∕v, le temps pour aller du point C (x₀,y₀) au point D le plus bas (θ = π) est

∘ --- R ∫ π∘ --1---cosθ---- t = -- -------------dθ g θ0 cosθ0 - cosθ

(14)

soit encore en posant u = cos θ
2 (et u₀ = cos θ0
2 )

∘ --- ∘ --- ∘ --- R ∫ u0 du R [ x ]u0 R t = 2 -- ∘---------= 2 -- arcsin --- = --π g 0 u20 - u2 g u0 0 g

(15)

donc le temps pour atteindre le point le plus bas ne dépend pas du point de départ, c’est une courbe tautochrone !

2.4.2 Isochronie

Cette propriété se déduit de la tautochronie, la période du pendule cycloïdal vaut T = 4 ∘ ---
R
-g π = 2π ∘ ----
2R
-g- , elle est indépendante de l’amplitude des oscillations. Par ailleurs, cela correspond bien à la période d’un pendule simple de longueur 2R dans l’approximation des faibles amplitudes d’oscillation (le cercle osculateur à la cycloïde en son point le plus bas à pour rayon 2R).

[next] [prev] [prev-tail] [front] [up]