3 Étude numérique

3.1 Distance normalisée

À partir des équations (13) et (15) on peut tracer y = f(x) (figure 2).

Si on s’intéresse à la distance horizontale d parcourue par le projectile, il faut tout d’abord déterminer l’angle α_s pour lequel y s’annule. On peut utiliser pour cela un algorithme de type Newton, en partant d’une valeur initiale α_s = -α₀ qui correspond au cas sans frottement. On applique alors la formule

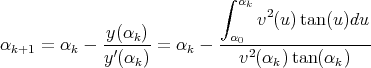(20)

jusqu’à ce que la valeur |α_k+1 - α_k| soit inférieure à une valeur fixée à l’avance, par exemple 0, 01∘. Une fois α_s déterminé, on calcule d = x(α_s) - x₀ à l’aide de l’équation (15), ce qui correspond à la distance parcourue horizontalement.

On peut constater d’après (20) que α_s ne dépend en fait que de α₀ et du rapport v₀∕v_lim que l’on appelera désormais vitesse normalisée et que l’on notera v_norm. De même, si on normalise d par la distance parcourue en l’absence de frottement, à savoir

(21)

alors d_norm = d∕d_ref est uniquement une fonction de α₀ et de v_norm, cette quantité normalisée peut par conséquent être calculée indépendamment de la valeur du rapport λ∕m. On obtient donc un résultat général à partir duquel l’influence des différents paramètres pourra aisément être étudiée. La distance normalisée est représentée sur la figure 3.

3.2 Paramétrisation

Afin de pouvoir étudier facilement d_norm, nous allons chercher à paramétriser cette fonction. Pour α₀ fixé, on observe que l’on peut décrire d_norm en fonction de v_norm à l’aide d’une fonction de Pearson VII (voir la figure 4 pour α₀ = 45∘) :

(22)

Pour M = 1, cette fonction est une lorentzienne, et pour M →∞, il s’agit d’une gaussienne (cf. annexe A).

Les paramètres K et M sont donc des fonctions de α₀, leurs variations respectives sont représentées sur les figures 5(a) et 5(b).

(a) Paramètre K (b) Paramètre M FIGURE 5: Paramètres K et M en fonction de l’angle de lancer α0.

Ces paramètres peuvent facilement être décrits par des polynômes P_N(α₀) = ∑ _i=0^i=Na _iα₀ⁱ de degrés 3 et 2, dont les coefficients a_i sont donnés dans la table 1.

À l’aide des coefficients de la table 1 et de l’équation (22), on retrouve les valeurs calculées pour obtenir la figure 3 avec une erreur relative inférieure à 0, 2%. On peut donc considérer que le calcul de la distance parcourue par un projectile a été considérablement simplifié par rapport au problème initial qui consistait à utiliser les équations (15) après avoir résolu (20). Les influences respectives de v₀, v_lim et α_O peuvent donc à présent être étudiées sans difficulté.

3.3 Exemple d’application

Nous nous intéressons à l’influence de l’angle de lancer sur la distance parcourue. En l’absence de frottement, la distance est donnée par la formule (21), elle est donc maximale pour α₀ = 45∘, et la distance parcourue sera la même pour α₀ = 45∘ ± φ, φ variant entre 0 et 45∘. Si l’on tient compte des frottements, la distance parcourue n’est plus symétrique par rapport à α₀ = 45∘, une étude rapide de la figure 3 semble indiquer que la distance sera plus grande pour les angles inférieurs à 45∘, ce qui est généralement ce que nous dicte notre intuition. Si cela est bien exact pour notre étude comme on le verra par la suite, il faut cependant se méfier de l’intuition pour des frottements en vⁿ avec n ≥ 3, 5 car l’angle optimal de lancer peut alors être supérieur à 45∘ [14].

Dans le cas présent, à partir du travail effectué dans la partie 3.2, il est facile de calculer d pour v₀ fixé en faisant varier l’angle α₀, puis de voir pour lequel de ces angles d est maximal. Nous avons effectué le calcul pour une balle de baseball avec λ∕m = 0, 005376 m-1, soit v _lim = 42, 7 m⋅s-1 [7, 12] et v ₀ = v_norm.v_lim, le résultat est présenté figure 6.

On constate bien que lorsque v₀ augmente, l’angle permettant d’obtenir la distance maximale diminue. La forme de la courbe nous incite à chercher une loi de comportement une nouvelle fois décrite pour une loi de Pearson : α_max = h^-M. On impose h = 45∘, et l’optimisation des deux autres paramètres conduit à K = 0, 0085864 s⋅m-1 et M = 0, 1366571, ce qui donne une erreur relative maximale inférieure à 0, 08% ! Le choix de cette fonction est donc validé.

Le lecteur curieux pourra vérifier qu’à l’aide des paramètres donnés dans la partie 3.2, il obtiendra aisément les résultats relatifs aux valeurs utilisées dans la référence [5], avec cependant un léger écart dû au fait que le rapport v₀∕v_lim dans cet ouvrage (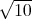 ≈ 3, 16) est près du double de la valeur maximale considérée ici pour la détermination des paramètres d’interpolation (1, 5).