|
|
On cherche à décrire la trajectoire d’un mobile M, de masse m, soumis à la pesanteur, en tenant compte de la résistance de l’air. Pour cela, on utilise le repère de Frénet (figure 1).
La vitesse initiale et l’angle de départ sont respectivement v0 et α0. Dans ce repère, le rayon de coubure vaut r = -ds∕dα, la vitesse v = ds∕dt = ds∕dα.dα∕dt = -rdα∕dt est portée par la tangente T à la trajectoire, et l’accélération se décompose sur T et sur la normale à la trajectoire N en
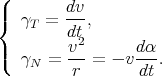 | (1) |
La résistance de l’air est caractérisée par une force R(v) qui s’oppose au mouvement, colinéaire à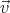 
mais
de sens opposé. Par conséquent, on obtient comme équations du mouvement :
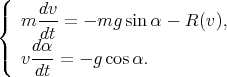 | (2) |
On en déduit
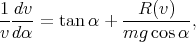 | (3) |
il s’agit de l’équation fondamentale de la balistique, parfois appelée «équation de l’hodographe» [9].
Pour R(v) = λvn, l’équation (3) est une équation différentielle de Bernoulli. On peut la résoudre par exemple grâce à une méthode proposée par Legendre [10, 11] (une autre méthode est présentée dans [12] directement pour n = 2, et historiquement Leibniz est le premier à avoir résolu ce type d’équation dès 1696). En posant
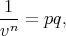 | (4) |
on obtient après différenciation -n
= pdq + qdp, et l’équation (3) peut se mettre sous la
forme
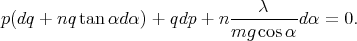 | (5) |
On annule le coefficient de p, ce qui conduit à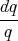 
= -n tan αdα, soit q = cos nα. On obtient alors
dp = -
n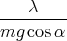
dα = -
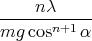dα, et par intégration
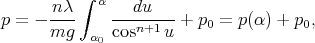 | (6) |
la constante p0 étant déterminée à l’aide des conditions initiales sur v. Pour α = α0, v(α) = v0, et
d’après (4)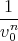 
= (p(α0) + p0).q = p0 cos nα
0 (car p(α0) = 0), on en déduit
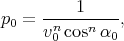 | (7) |
on peut alors expliciter la formule (4) :
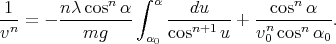 | (8) |
Comme on l’a précisé en introduction, la résistance de l’air peut être traitée avec n = 2.
On a donc p0 =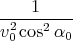 
et
![2λ--∫ α -du--- -λ--[ u- π- -sin-u-]α
p(α) = - mg α cos3u = - mg ln(tan( 2 + 4 )) + cos2 u ,
0 α0](dragforce18x.png) | (9) |
soit
![2 [ ]α 2
1-- λ-cos-α- u- π- -sin-u- --cos-α---
v2 = - mg ln(tan( 2 + 4 )) + cos2 u α + v20 cos2α0.
0](dragforce19x.png) | (10) |
Après un temps suffisamment long, on sait que α doit tendre vers -π∕2. On peut donc trouver la vitesse limite de chute :
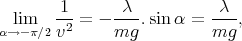 | (11) |
on retrouve ainsi le résultat connu dans le cas d’une chute libre [13], à savoir
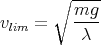 | (12) |
(les forces de frottement compensent la gravitation, la vitesse reste donc constante).
On a donc pour finir
![2 ------(---------------v20-cos2α0--------------------)--
v (α) = 2 [ ] α .
cos2α 1 - -v0-cos2 α0 ln (tan (u-+ π-)) + sinu--
v2lim 2 4 cos2u α0](dragforce22x.png) | (13) |
Le calcul de la position se fait à l’aide des équations
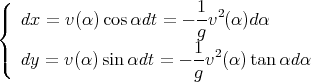 | (14) |
et par intégration on trouve
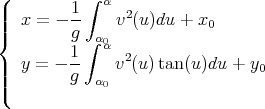 | (15) |
En conclusion, on est passé du système d’équations différentielles couplées (2) et (14)
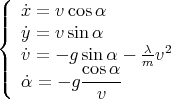 | (16) |
à une formule analytique (13) et deux calculs d’intégrales (15) pour obtenir x et y. Nous allons donc pouvoir étudier l’influence des frottements sur la distance que peut parcourir un projectile.
Bien que cela ne soit en rien utile à la suite de l’étude, il est intéressant de constater qu’à partir des équations déjà établies, on peut assez facilement déterminer l’abscisse curviligne s parcourue en fonction de α [12]. En effet, en comparant (1) et (2), et en utilisant le fait que ds = -rdα, on obtient
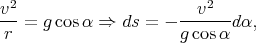 | (17) |
et donc avec (13)
![∫ α -------(--------------v20-cos2α0---------------------)--
ds = - α v2 [ u π sinu ]α d α.
0 gcos3α 1 - -20-cos2 α0 ln(tan (--+ --)) +------
vlim 2 4 cos2 u α0](dragforce27x.png) | (18) |
Or d’après (9), l’intégrand dans (18) est de la forme u′∕u, et ds peut donc s’intégrer aisément sous la forme
![( [ ] )
v2lim- -v20- 2 u- π- sinu-- α
s = 2g ln 1 - v2 cos α0 ln (tan (2 + 4 )) + cos2u .
lim α0](dragforce28x.png) | (19) |
Il semble que Euler soit le premier à avoir obtenu cette expression (voir l’avant-propos dans [2]).
