|
|
L’inclinaison de l’axe de la Terre (obliquité) est ε = 23∘26′ = 23, 43∘. La longitude écliptique du Soleil au périhélie par rapport au point vernal (noté γ) est Π = 282, 9372∘ (figure 13).
La longitude écliptique du Soleil (plan de l’écliptique : plan de rotation du soleil) est donnée par :
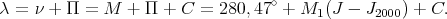 | (33) |
Dans le système de coordonnées écliptiques, le Soleil a pour coordonnées
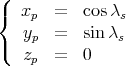 | (34) |
On veut maintenant exprimer les coordonnées du Soleil dans le système de coordonnées équatoriales. Ces coordonnées sont nommées ascension droite (α) et déclinaison (δ). Dans ce système, le Soleil a pour coordonnées
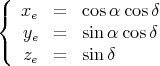 | (35) |
et à l’aide d’une matrice de rotation (rotation d’un angle -ε autour de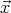 
), on obtient sans trop de difficulté à
partir de l’équation (34)
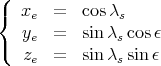 | (36) |
soit finalement en rassemblant les équations (35) et (36)
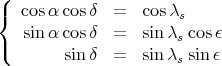 | (37) |
et donc
On peut utiliser directement ces deux formules (en faisant attention à l’utilisation de la fonction arctan [4]), ou utiliser un développement limité en ε. On obtient alors
On peut vérifier que -ε < δs < ε.On appelle R la différence entre αs et λs :
Après calcul on obtient
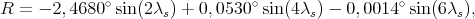 | (43) |
et
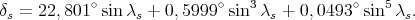 | (44) |
On trouve dans la littérature une autre expression pour R (par exemple [4], avec une démonstration différente).
Soit y = arctan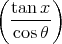 
. Dans [2], il est montré que
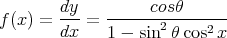 | (45) |
peut s’exprimer sous la forme d’une série de Fourier :
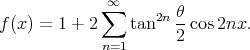 | (46) |
Par intégration, on peut alors exprimer y sous forme d’une somme.
Considérons à présent la fonction y = arctan(tan x. cos θ). Sa dérivée vaut
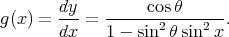 | (47) |
On a donc g(x) = f(x - π∕2). Par conséquant, on peut écrire
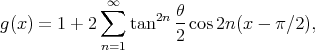 | (48) |
soit encore, sachant que cos nπ = (-1)n (n entier) :
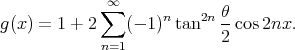 | (49) |
Par intégration et remplacement des variables par les quantités pertinentes pour le problème (équation (38), on obtient donc finalement
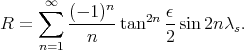 | (50) |
Généralement, la formule présentée ne retient que trois termes :
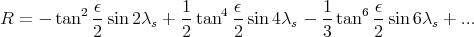 | (51) |
On peut remarquer que l’équation (42) correspond au développement limité à l’ordre 6 de l’équation (51). L’application numérique donne un résultat identique.
