[next] [prev] [prev-tail] [tail] [up]

B Relation entre l’anomalie vraie et l’anomalie moyenne

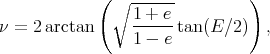
L’anomalie vraie ν est reliée à l’anomalie excentrique E par la relation

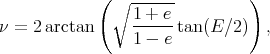( ------ ) ∘ 1 + e ν = 2 arctan -----tan(E ∕2) , 1 - e
(24)

avec e l’excentricité de la trajectoire. Un développement limité en e à l’ordre 3 donne

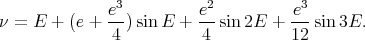e3 e2 e3 ν = E + (e + --)sin E + --sin 2E + ---sin3E. 4 4 12
(25)

Par ailleurs, l’anomalie excentrique E est reliée à l’anomalie moyenne M par l’équation de Kepler :

E = M + e sin E.
(26)

On peut la résoudre à l’aide du théomème d’inversion de Lagrange, qui pour une variable z définie par z = x + yf(z) permet d’exprimer toute fonction G(z) comme une série de puissances de y :

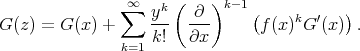∞ k ( )k- 1 ∑ y-- -∂- ( k ′ ) G (z) = G (x ) + k! ∂x f(x) G (x ) . k=1
(27)

Dans notre cas, z = E, G(z) = z, G′(z) = 1, x = M, y = e et f(z) = sin E, on en déduit

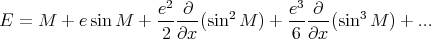e2-∂- 2 e3-∂- 3 E = M + esinM + 2 ∂x (sin M ) + 6 ∂x (sin M ) + ...
(28)

soit après linéarisation

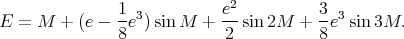1- 3 e2 3-3 E = M + (e - 8 e )sin M + 2 sin 2M + 8e sin3M.
(29)

En combinant les équations (25) et (29), on obtient enfin une relation entre l’anomalie vraie et l’anomalie moyenne :

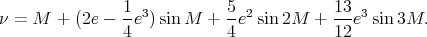1 3 5 2 13 3 ν = M + (2e - 4-e )sinM + 4e sin2M + 12e sin 3M.
(30)

Remarque : dans le cadre d’un calcul purement numérique, l’équation (24) peut bien évidemment être utilisée directement si l’on connait E, cependant l’équation (26) doit toujours être résolue pour trouver E. Pour ce faire, on peut utiliser un algorithme de type Newton pour chercher une racine de la fonction f(E) = M - E + e sin E. L’algorithme de Newton pour la recherche d’une solution à l’équation f(x) = 0 s’écrit

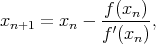f(xn ) xn+1 = xn - f′(x-), n
(31)

par conséquent on résout l’équation (26) par itération à l’aide de la formule

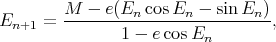M----e(En-cosEn----sin-En-) En+1 = 1 - ecosE , n
(32)

qui en partant de E0 = M converge rapidement.

[next] [prev] [prev-tail] [front] [up]