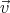1.5 Coordonnées curvilignes
On choisit un nouveau repère attaché au point M, à savoir (M, τ,
τ, N), où
N), où  τ est tangent à la
trajectoire,
τ est tangent à la
trajectoire,  N est tel que
N est tel que  τ.
τ. N = 0 (donc obtenu par rotation de π∕2 dans le sens direct
du vecteur
N = 0 (donc obtenu par rotation de π∕2 dans le sens direct
du vecteur  τ). Localement, le cercle osculateur à la trajectoire (cercle qui décrit au
mieux la courbure de l’arc ds) a pour rayon R, on peut écrire ds = Rdφ et on montre
que
τ). Localement, le cercle osculateur à la trajectoire (cercle qui décrit au
mieux la courbure de l’arc ds) a pour rayon R, on peut écrire ds = Rdφ et on montre
que
 | (1.16) |
À partir de l’abscisse curviligne s (longueur de la trajectoire de M depuis l’origine M0), on
peut déduire
 | (1.17) |
même si bien souvent, on détermine s à partir de ṡ = ||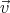 || (voir l’exemple de la cycloïde) :
|| (voir l’exemple de la cycloïde) :
 | (1.18) |
 | (1.19) |
L’accélération peut également s’écrire
 | (1.20) |
avec
 τ,
τ, N), où
N), où  τ est tangent à la
trajectoire,
τ est tangent à la
trajectoire,  N est tel que
N est tel que  τ.
τ. N = 0 (donc obtenu par rotation de π∕2 dans le sens direct
du vecteur
N = 0 (donc obtenu par rotation de π∕2 dans le sens direct
du vecteur  τ). Localement, le cercle osculateur à la trajectoire (cercle qui décrit au
mieux la courbure de l’arc ds) a pour rayon R, on peut écrire ds = Rdφ et on montre
que
τ). Localement, le cercle osculateur à la trajectoire (cercle qui décrit au
mieux la courbure de l’arc ds) a pour rayon R, on peut écrire ds = Rdφ et on montre
que