
Choisissons une accélération décrite par
 | (4.13) |
(μ > 0, donc l’accélération est bien dirigée vers le centre O). Dans ces conditions, en posant
u =  , on obtient avec la deuxième formule de Binet (4.12)
, on obtient avec la deuxième formule de Binet (4.12)
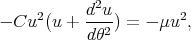 | (4.14) |
soit encore
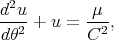 | (4.15) |
et la solution est
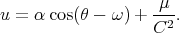 | (4.16) |
En posant e = αC2∕μ, on trouve finalement
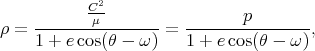 | (4.17) |
ce qui est l’équation d’une conique d’excentricité e et de paramètre p. Les constantes arbitraires α et ω introduite dans (4.16) sont déterminées à partir des conditions initiales, et il est toujours possible de choisir α > 0 et donc e > 0, car si on obtient α < 0, il suffit alors de remplacer ω par ω + π [1].
Utilisons à présent la première formule de Binet,
et finalement on en déduit
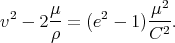 | (4.23) |
Le second membre est constant, on en déduit donc que le premier membre l’est également, et que par conséquent sa valeur ne dépend que des valeurs initiales de v et de ρ. Plus précisément, ce sont ces valeurs initiales qui vont déterminer le type de trajectoire, à savoir
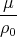 < 0, alors e2 - 1 < 0, la trajectoire est une ellipse,
< 0, alors e2 - 1 < 0, la trajectoire est une ellipse,
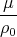 = 0, alors e2 - 1 = 0, la trajectoire est une parabole,
= 0, alors e2 - 1 = 0, la trajectoire est une parabole,
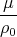 > 0, alors e2 - 1 > 0, la trajectoire est une hyperbole.
> 0, alors e2 - 1 > 0, la trajectoire est une hyperbole.Il est remarquable que pour une distance initiale ρ0, seule le module de la vitesse détermine le type de la trajectoire, et en aucun cas sa direction [2].
Le cas où la trajectoire est une ellipse correspond à la première loi de Kepler. Ce cas nous permet également de retrouver la troisième loi de Kepler. Par intégration sur une période T, l’équation (4.4) donne
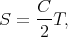 | (4.24) |
et la trajectoire étant une ellipse, on sait aussi que
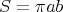 | (4.25) |
où a et b sont les demi grand axe et demi petit axe de l’ellipse. On montre par ailleurs
que b = 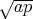 avec p le paramètre de l’ellipse, déjà défini par l’équation (4.17), on en
déduit
avec p le paramètre de l’ellipse, déjà défini par l’équation (4.17), on en
déduit
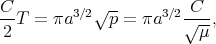 | (4.26) |
ce qui conduit après élévation au carré à
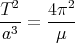 | (4.27) |
Or μ étant une constante caractéristique de la cause de l’accélération, on en déduit bien la
troisième loi de Kepler, qui dit que le rapport T2∕a3 est constant pour les planètes gravitant
autour du Soleil.
Remarque : on a supposé auparavant μ > 0, mais pour les forces coulombiennes, il est possible
d’avoir μ < 0. Dans ce cas, on a toujours v02 - 2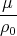 > 0, et la trajectoire d’une particule chargée
subissant une accélération due à une particule chargée de même signe sera une branche
d’hyperbole.
> 0, et la trajectoire d’une particule chargée
subissant une accélération due à une particule chargée de même signe sera une branche
d’hyperbole.