
The problem of the two-dimensional motion of a projectile being only subject to the gravity is well known by student, and the determination of its trajectory is a trivial task. If a drag force proportional to the velocity is taken into account, the problem can still be analytically solved. On the other hand, the case of a quadratic drag force is most of the times only solved numerically [1], except in the one-dimensional case [2, 3]. Indeed, an analytical solution does not exist for the position in the two-dimensional case, but approximate solutions for particular cases have been proposed [4, 5, 6].
Whether the linear or the quadratic case has to be considered actually depends on the dimensionless Reynolds number Re. The linear case holds for Re < 1, whereas the quadratic case is valid when 103 < Re < 2.105 [3]. As an example, for a spherical object of diameter 5 cm (like a baseball) in air, the first condition on Re is met if the velocity of the object is below 0.3 mm⋅s-1, and the second condition is met for velocities between 0.25 m⋅s-1 and 53 m⋅s-1. It is then clear that quadratic drag forces are more likely to be observed by students during physics practical works, and taking them into account should improve the theory-experiment agreement.
The solution to the problem of finding the position in the two-dimensional case requires the resolution of four coupled differential equations, but can be simplified to the computation of only two numerical integrations, after an analytical solution for the velocity is obtained. We now briefly review the main steps of this simplification.
Let’s consider a drag force R(v) = λvn, the equations of motion are
 | (1) |
where α is the slope of the velocity vector. The position is obtained through the solutions of
 | (2) |
From Eq. (1), we can deduce hodograph equation [7]
 | (3) |
which solution is
 | (4) |
As we actually consider a quadratic drag force, we set n = 2 and obtain
![[ ]
-1 λcos2α- u- π- sinu- α --cos2-α-
v2 = - mg ln(tan(2 + 4))+ cos2 u α + v20 cos2α0 .
0](drag_html4x.png) | (5) |
After a sufficient long time, α should reach the value -π∕2, thus we can find the limit of the velocity:
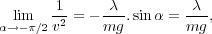 | (6) |
which is the result obtained for the one-dimensional case [3] and we define vlim as
 | (7) |
(the drag force and the gravity compensate each other, the velocity is constant). We thus finally get [1]
![v2(α) = -----(-------------v20cos2α0-----------------)-,
v20 2 [ u π sin u ]α
cos2 α 1- v2--cos α0 ln(tan(2-+ 4))+ cos2u-
lim α0](drag_html7x.png) | (8) |
and the position can be calculated after insertion of the second line of Eq. (1) in Eq. (2):
 | (9) |
An exemple of trajectories in the absence and with a quadratic drag force is depicted on Fig. 1.