Rotation autour d’un axe

[next] [prev] [prev-tail] [tail] [up]

2.3 Rotation autour d’un axe

On suppose que le référentiel R′ est en rotation autour d’un axe fixe Δ dans R. On choisit z et z′ de sorte à ce qu’ils soient confondus avec l’axe de rotation Δ. Les origines O et O′ sont confondues, ainsi que les plans définis par x,y et x′,y′.

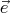Dans le repère R, OM⃗ = xx +yy +zz, et dans le repère tournant R′, O⃗M = x′x′ +y′y′ +z′z′. On appelle φ l’angle que font les vecteurs x,x′ et y,y′.

On définit le vecteur 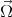porté par l’axe de rotation et de module (vitesse angulaire de rotation du repère R′ par rapport à R). Donc

⃗Ω = φ˙⃗ez

(2.7)

et on montre que

d⃗ex′ d⃗ey′ ---- = ⃗Ω ∧ ⃗ex′,---- = ⃗Ω ∧ ⃗ey′. dt dt

(2.8)

La position de M dans R′ s’exprime comme

O⃗M = x′⃗ex′ + y′⃗ey′ + z′⃗ez′.

(2.9)

La loi de composition des vitesses s’obtient en dérivant la relation (2.9) par rapport au référentiel R :

dOM⃗-- dx′ dy′ dz′ ′d-⃗ex′ ′d⃗ey′ dt |R= dt ⃗ex′ + dt ⃗ey′ + dt ⃗ez′ + x dt + y dt ,

(2.10)

d’où

⃗v = ⃗v ′ + ⃗v , M∕R M ∕R e

(2.11)

avec la vitesse de M dans R′

′ ′ ′ ′ dx- ′ dy- ′ dz- ′ ⃗vM∕R = dt ⃗ex + dt ⃗ey + dt ⃗ez,

(2.12)

et e la vitesse d’entraînement :

⃗ve = ⃗Ω ∧ O⃗M .

(2.13)

Pour l’accélération, on dérive dans R la relation (2.10) et on trouve

⃗γ = ⃗γ ′ + ⃗γ + ⃗γ , M ∕R M ∕R e c

(2.14)

avec l’accélération de M dans R′ :

d2x′ d2y′ d2z′ ⃗γM ∕R′ = dt2-⃗ex′ + dt2-⃗ey′ +-dt2 ⃗ez′,

(2.15)

l’accélération d’entraînement e (qui n’est pas la dérivée de la vitesse d’entraînement e) :

′d2⃗ex′ ′d2⃗ey′ d-⃗Ω ⃗ ⃗ ⃗ ⃗ ⃗γe = x dt2 + y dt2 = dt ∧ OM + Ω ∧ (Ω ∧ OM ),

(2.16)

et l’accélération de Coriolis :

⃗ ⃗ ⃗γc = 2Ω ∧ ⃗vM ∕R′ = 2 Ω ∧ (⃗vM∕R - ⃗ve).

(2.17)

[next] [prev] [prev-tail] [front] [up]