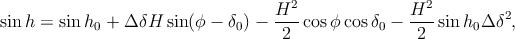
Afin de calculer la variation de hauteur du Soleil entre son passage au méridien et l’angle horaire H déterminé auparavant, repartons de l’équation (1), mais en explicitant δ = δ0 + ΔδH , en développant les termes en sin δ et cos δ et en effectuant un développement limité à l’ordre 2 des termes en cos H. Après quelques lignes de calcul, on obtient :
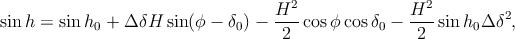 | (12) |
avec
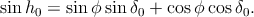 | (13) |
Si l’on remplace H par son expression donnée par l’équation (10), on voit que le dernier terme obtenu dans (12) est en Δδ4, alors que les deux termes précédents sont en Δδ2. On va donc pouvoir négliger ce dernier terme par rapport aux deux autres. Par conséquent, en n’oubliant pas que sin(ϕ - δ0) = sin z = cos h0 , on trouve pour finir
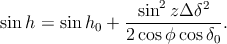 | (14) |
Comme par ailleurs, on peut écrire
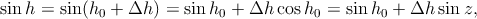 | (15) |
on en déduit pour finir
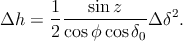 | (16) |
Encore une fois, ce résultat diffère légèrement de celui donné par D. Savoie dans son ouvrage, qui est en tan Δz, mais Δz (ou Δh) étant très petit, il n’y a pas de différence notable dans l’application numérique.