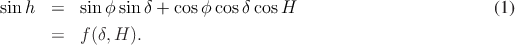
On part de la formule reliant la hauteur h du Soleil pour une latitude ϕ à sa déclinaison δ et à l’angle horaire H :
sin h étant une fonction croissante de h si 0 < h < π∕2, on peut étudier directement la fonction f pour trouver le maximum de h. Celui-ci s’obtient en écrivant df = 0, soit en explicitant : et donc pour finir
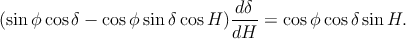 | (3) |
En utilisant la notation de D. Savoie Δδ =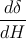 
(variation horaire de la déclinaison), on a
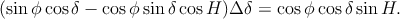 | (4) |
Il s’agit d’une équation transcendante, que l’on peut résoudre par itération. Cependant, il y a plus simple. Δδ étant très faible (δ et H sont deux fonctions du temps, mais δ varie d’environ 46∘ en six mois, alors que H varie de 15∘ par heure), on peut déduire de (4) que sin H et donc H le sera également. Par conséquent, on peut considérer que cos H ≈ 1, ce qui permet de simplifier le membre de gauche de (4) :
et permet donc d’obtenir la relation On peut également se contenter de la première simplification (5), ce qui donne
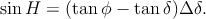 | (8) |
La formule (7) diffère légèrement de celle donnée par D. Savoie, qui est en tan H. Cependant, cette différence est en réalité négligeable, car comme on l’a dit auparavant, H étant très petit, on peut utiliser l’approximation sin H ≈ tan H ≈ H sans modification sensible du résultat, ce qui conduit à la formule « définitive » donnant l’angle horaire de culmination du Soleil
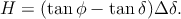 | (9) |
Cette équation est toujours une équation transcendante, puisque δ n’est pas une constante, cependant sa variation temporelle est tellement faible par rapport à celle de H qu’il est inutile de procéder à plusieurs itérations pour affiner la valeur de H, le calcul direct est suffisant, en utilisant δ = δ0, c’est-à-dire la valeur de la déclinaison au méridien.
On peut introduire la distance zénithale du Soleil au méridien z = ϕ-δ0, qui permet d’écrire (7) sous la forme
 | (10) |
Les jours d’équinoxe, la formule (9) peut encore se simplifier en considérant la déclinaison comme pratiquement nulle, ce qui conduit à
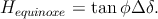 | (11) |
Utilisons cette dernière formule pour retrouver les résultats fournis par D. Savoie : on se place le 21 mars 2003 (équinoxe de printemps), on a Δδ = 1′∕15∘. À Paris (ϕ = 48∘50′11′′), on trouve H = 17s, au Caire (ϕ = 30∘) on obtient H = 9s, et pour ϕ = 60∘ on a H = 26s. Ces valeurs correspondent bien à celles données dans l’ouvrage cité.
