2 Test du
 2
2
3 Test de Smirnov-Kolmogorov
4 Intervalles de confiance
4.1 Pour une nouvelle mesure
4.2 Pour la valeur mesurée
5 Formules mathématiques
6 Conclusion
7 Version
 2
2
Octave est un logiciel libre en grande partie compatible avec le logiciel commercial MatlabTM. Il est disponible sur le site http://www.octave.org. Pour tracer les graphiques, il utilise le logiciel Gnuplot (http://www.gnuplot.info). De nombreuses fonctions statistiques sont intégrées à Octave, seules certaines d’entre elles seront présentées et utilisées dans ce document.
Soit un fichier mesures.dat contenant N valeurs, on charge le fichier en mémoire et on trie les valeurs par ordre croissant :
|
On peut alors très simplement calculer la valeur moyenne des valeurs, l’écart-type sans biais, les valeurs centrées réduites ainsi que l’incertitude-type de type A.
|
 2
2Pour effectuer un test du  2, il faut tout d’abord déterminer le nombre de classes.
2, il faut tout d’abord déterminer le nombre de classes.
|
On détermine ensuite les bornes de chacun des intervalles :
|
On calcule alors les fréquences pour chacune des classes.
|
On cherche les fréquences théoriques. Celles-ci sont obtenues à partir de la fonction de cumul de la loi normale (figures 1 et 2).
|
On peut alors calculer la valeur totale  2, et en déduire la probabilité
2, et en déduire la probabilité  de commettre une erreur en
rejetant l’hypothèse gaussienne.
de commettre une erreur en
rejetant l’hypothèse gaussienne.
|
Connaissant  2 et le nombre de degrés de liberté L = NCl - 3, on est donc capable de calculer
2 et le nombre de degrés de liberté L = NCl - 3, on est donc capable de calculer  .
Octave fournit également la fonction chisquare_inv qui calcule
.
Octave fournit également la fonction chisquare_inv qui calcule  2 à partir de L et
2 à partir de L et  (c’est cette
fonction qui peut être utilisée pour remplir la table du
(c’est cette
fonction qui peut être utilisée pour remplir la table du  2). Les fonctions implémentées dans Octave
travaillent en fait sur la quantité 1 -
2). Les fonctions implémentées dans Octave
travaillent en fait sur la quantité 1 -  , on aura donc 1 -
, on aura donc 1 -  =chisquare_cdf(
=chisquare_cdf( 2,L) et
2,L) et
 2 =chisquare_inv(1 -
2 =chisquare_inv(1 -  ,L).
,L).
Pour le test de Smirnov-Kolmogorov, on calcule tout d’abord les cumulants, en tenant compte du cas particulier des valeurs multiples.
|
Le cumul théorique (figure 2) est ensuite calculé, afin d’obtenir l’écart avec le cumul obtenu précédemment, et l’écart maximal de ||F - Fn*|| est recherché.
|
Il nous faut à présent, comme pour le test du  2, calculer la probabilté
2, calculer la probabilté  SK de commettre une
erreur en rejetant l’hypothèse gaussienne. Pour cela, Octave nous propose deux fonctions. La
première fonction est kolmogorov_smirnov_cdf(x). Or la table disponible dans la
littérature donnant
SK de commettre une
erreur en rejetant l’hypothèse gaussienne. Pour cela, Octave nous propose deux fonctions. La
première fonction est kolmogorov_smirnov_cdf(x). Or la table disponible dans la
littérature donnant  SK en fonction du nombre de mesures et de l’écart maximal des cumulants
comporte deux entrées. L’explication est que la fonction définie par Octave n’est que la formule
asymptotique pour le calcul de la probabilité, prenant comme argument
SK en fonction du nombre de mesures et de l’écart maximal des cumulants
comporte deux entrées. L’explication est que la fonction définie par Octave n’est que la formule
asymptotique pour le calcul de la probabilité, prenant comme argument  .max||F - F
n*||,
cette formule étant valable pour un nombre de mesures n supérieur à 35 ou 100 selon les
auteurs.
.max||F - F
n*||,
cette formule étant valable pour un nombre de mesures n supérieur à 35 ou 100 selon les
auteurs.
 | (1) |
La deuxième fonction présente dans Octave s’utilise de la manière suivante :
[ SK, ks] = kolmogorov_smirnov_test(vcr, "normal", "<>") . Elle prend
donc directement les valeurs centrées réduites des mesures en argument, et retourne
SK, ks] = kolmogorov_smirnov_test(vcr, "normal", "<>") . Elle prend
donc directement les valeurs centrées réduites des mesures en argument, et retourne  SK et
ks=
SK et
ks=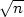 .max||F - F
n*||. Cette deuxième fonction est donc légèrement plus directe que la première
présentée, mais elle souffre du même défaut.
.max||F - F
n*||. Cette deuxième fonction est donc légèrement plus directe que la première
présentée, mais elle souffre du même défaut.
La solution consiste donc à implémenter la véritable fonction donnant  SK. Cette fonction est
définie par la formule suivante :
SK. Cette fonction est
définie par la formule suivante :
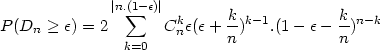 | (2) |
où |x| représente la partie entière de x.
On va donc créer la fonction skbl.m (pour Smirnov-Kolmogorov bilatéral).
|
Il est donc à présent trivial de calculer  SK en faisant appel à cette routine.
SK en faisant appel à cette routine.
|
On peut remarquer que si l’on sait à présent calculer  SK à partir de n et de l’écart maximal, on ne
connaît pas la fonction inverse permettant d’obtenir la table de Smirnov-Kolmogorov. En fait, cette
fonction n’existe pas, on est obligé de procéder par dichotomie. L’algorithme suivant permet de calculer
la table de Smirnov-Kolmogorov telle que publiée dans [Mesure physique et instrumentation, D.
Barchiesi, Ellipses, 2003].
SK à partir de n et de l’écart maximal, on ne
connaît pas la fonction inverse permettant d’obtenir la table de Smirnov-Kolmogorov. En fait, cette
fonction n’existe pas, on est obligé de procéder par dichotomie. L’algorithme suivant permet de calculer
la table de Smirnov-Kolmogorov telle que publiée dans [Mesure physique et instrumentation, D.
Barchiesi, Ellipses, 2003].
|
On peut remarquer que pour des valeurs de  = max||F - Fn*|| faibles, l’équation 2 donne un
résultat supérieur à 1 !
= max||F - Fn*|| faibles, l’équation 2 donne un
résultat supérieur à 1 !
On cherche à déterminer l’intervalle dans lequelle on aura P% de chance d’obtenir une nouvelle
mesure. Si l’on suppose la répartition des mesures gaussiennes, alors l’intervalle est : [ -k
-k ;
; + k
+ k ]
avec
]
avec  la valeur moyenne des mesures,
la valeur moyenne des mesures,  l’écart-type sans biais et k le facteur d’élargissement obtenu
à l’aide du code suivant :
l’écart-type sans biais et k le facteur d’élargissement obtenu
à l’aide du code suivant :
|
On pourra vérifier que pic=stdnormal_cdf(k1)*2-1.
On cherche à déterminer l’intervalle dans lequelle on aura P% de chance d’obtenir la valeur mesurée. Si
l’on suppose la répartition des mesures gaussiennes, alors la valeur moyenne suit la loi de Student
(figure 3) et l’intervalle est : [ - k
- k ;
; + k
+ k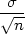 ] avec
] avec  la valeur moyenne des mesures,
la valeur moyenne des mesures,  l’écart-type sans biais, n le nombre de mesures et k le facteur d’élargissement obtenu à
l’aide du code suivant (le calcul fait apparaître la quantité n - 1 qui est le degré de liberté
L) :
l’écart-type sans biais, n le nombre de mesures et k le facteur d’élargissement obtenu à
l’aide du code suivant (le calcul fait apparaître la quantité n - 1 qui est le degré de liberté
L) :
|
Les fonctions de répartitions ou de cumul présentées dans les paragraphes précédents sont calculables
directement à l’aide des formules qui suivent. Par contre, comme dans le cas de la distribution de
Smirnov-Kolomogorov, les fonctions inverses font appel à des algorithmes plus complexes qu’un calcul
d’intégrale, et ne sont pas décrites ici.
Moyenne :  =
=  i=1Nm
i.
i=1Nm
i.
Écart-type sans biais :  N =
N = 
Valeur centrée réduite : 
stdnormal_pdf(x) :  e-x2/2
e-x2/2
stdnormal_cdf(x) :  (1 + erf(x/
(1 + erf(x/ )) avec erf(z) =
)) avec erf(z) = 
 t=0ze-t2
dt, soit après changement
de variable
t=0ze-t2
dt, soit après changement
de variable  = t
= t pour le calcul de l’intégrale erf(z) =
pour le calcul de l’intégrale erf(z) =  +
+ 

 =0ze-
=0ze- 2/2d
2/2d
t_pdf(x,n) :  avec
avec  (a,b) =
(a,b) =  et
et  (z) =
(z) =  t=0
t=0 tz-1e-tdt
tz-1e-tdt
Il est possible d’améliorer les codes présentés en rajoutant le tracé des histogrammes, des cumulants,...
$Id: stat_octave.tex,v 1.7 2004/11/16 13:10:27 alex Exp $
 2 et de la probabilité
2 et de la probabilité 
 SK
SK