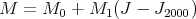
On plante un bâton verticalement dans le sol, qu’observe-t-on au fur et à mesure que le temps passe ? Jour après jour à heure fixe, comment se déplace l’ombre ? Et si on incline le bâton, quelle influence cela a-t-il ?
Pour le savoir, il faut dans un premier temps déterminer la trajectoire du Soleil par rapport à la Terre, puis calculer la position de l’ombre du bâton sur le sol. Au passage, on découvre pourquoi le jour le plus long, le Soleil ne se lève pas le plus tôt ni ne se couche le plus tard, pourquoi le Soleil ne se lève pas forcément à l’Est ni ne se couche à l’Ouest.
La Terre tourne autour du soleil, mais vu de la Terre, on dirait plutôt que c’est le soleil qui tourne.
L’anomalie moyenne M donne la position d’une planète par rapport à son périhélie si l’on considère que sa trajectoire est un cercle. On calcule donc d’abord l’anomalie moyenne M en fonction du jour julien J [1]
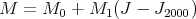 |
(1) |
avec J2000 = 2451545, M0 = 357, 5291∘ et M 1 = 0, 98560028∘∕jour pour la Terre. Comme une année dure environ 365, 25 jours, et que la Terre parcourt 360∘ en un an, on obtient donc M1 ≈ 360∕365, 25. La valeur de M0 provient du fait que la Terre est au périhélie aux alentours du 3 janvier. La conversion d’une date du calendrier classique (calendrier grégorien) en jour julien est détaillée dans l’annexe A. L’utilisation des jours julien permet une numérotation continue des jours, indépendamment de la durée des années.
Dans les faits, la trajectoire de la Terre est une ellipse. Pour tenir compte de l’ellipticité de la trajectoire, on doit corriger M d’une quantité C déterminée à l’aide de l’équation du centre, de manière à obtenir l’anomalie vraie ν :
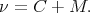 |
(2) |
Pour cela on doit résoudre l’équation de Kepler (en radians) :
 |
(3) |
(on procède par itérations, car il s’agit d’une équation transcendante, qui n’a a priori pas de solution analytique).
L’anomalie excentrique E est reliée à ν par l’équation suivante :
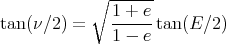 |
(4) |
Après un développement limité à l’ordre 3 en e de l’équation (4) (en appliquant trois fois l’équation (3)), on obtient :
 |
(5) |
soit encore :
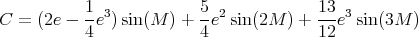 |
(6) |
Connaissant l’excentricité e = 0, 01671, on trouve (en degrés)
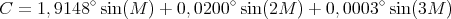 |
(7) |
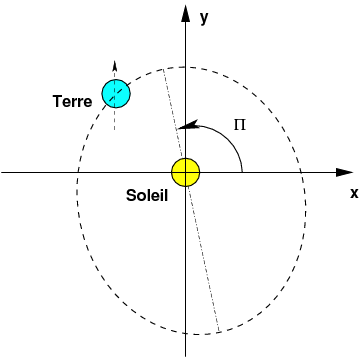
L’inclinaison de l’axe de la Terre (obliquité) est ε = 23∘27′ = 23, 45∘. La longitude écliptique du périhélie de la Terre est Π = 102, 9372∘ (figure 1).
|
La longitude écliptique de la Terre (plan de l’écliptique : plan de rotation du soleil) est donnée par :
 |
(8) |
Si l’on regarde le soleil depuis la terre, il y a 180∘ de différence, et donc
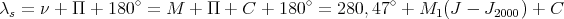 |
(9) |
Dans ce plan, on a
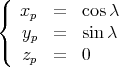 |
(10) |
|
On veut maintenant exprimer la position du soleil dans le système de coordonnées équatoriales (figure 2(a)). Les coordonnées sont nommées ascension droite (α) et déclinaison (δ). Dans ce système, la position du Soleil est donc :
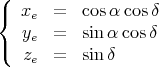 |
(11) |
et à l’aide d’une matrice de rotation (rotation d’un angle -ε autour de 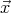 ), on obtient
sans trop de difficulté à partir de l’équation (10)
), on obtient
sans trop de difficulté à partir de l’équation (10)
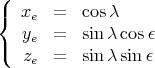 |
(12) |
soit finalement en rassemblant les équations (11) et (12)
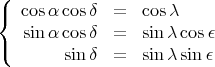 |
(13) |
et donc :
On peut utiliser directement ces deux formules, ou utiliser un développement limité en ε. On obtient alors
On peut remarquer que -ε < δs < ε.
On appelle R la différence entre αs et λs :
Après calcul on obtient :
 |
(19) |
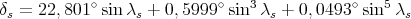 |
(20) |
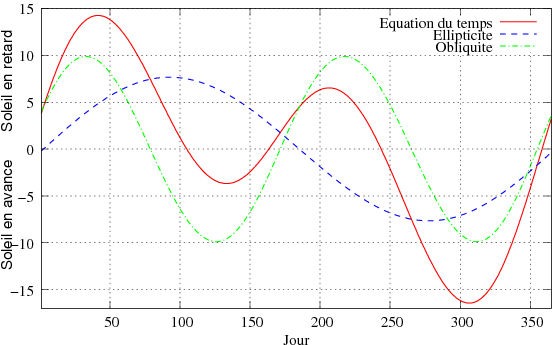
Nous avons vu précédemment que du fait de l’ellipticité de la trajectoire de la Terre et de l’inclinaison de son axe de rotation par rapport au plan de l’écliptique, deux corrections devaient être introduites pour calculer la position du soleil par rapport au cas idéal d’un mouvement circulaire dans le plan de l’écliptique. La somme de ces deux corrections, appelée «Équation du temps», donne l’écart ΔT (en minutes) entre le temps moyen et le temps vrai.
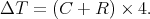 |
(21) |
Lorsque l’équation du temps est positive, le soleil est en retard sur l’horloge, et lorsque l’équation du temps est négative, le soleil est en avance sur l’horloge.
|
Nous avons calculé la position du soleil sur l’écliptique, puis dans le plan équatorial. Nous pouvons à présent calculer sa position telle qu’elle est perçue par un observateur situé à la latitude φ et à la longitude λL.
Dans le plan équatorial, on note H l’angle horaire, c’est-à-dire l’angle que fait le soleil avec le méridien local. Ainsi H = 0 à midi vrai (par définition), et la Terre efectuant une rotation de 360∘ en 24 heures, H = 15∘ à 13 heures, H = 30∘ à 14 heures et ainsi de suite. On va donc convertir H et δs (l’angle horaire et la déclinaison) en ce qu’on appelle l’azimuth et l’élévation, respectivement notés A et h, qui donnent la position du soleil par rapport à l’observateur (figure 2(b)). On a donc :
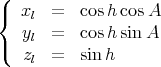 |
(22) |
Par ailleurs, dans le repère local ayant comme équateur l’équateur céleste et comme méridien origine la direction du Sud (méridien local), la position du Soleil s’écrit en fonction de H :
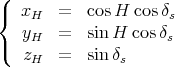 |
(23) |
Le plan local étant incliné de -(π∕2 - φ) par rapport au plan équatorial, on obtient
après rotation autour de 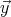 :
:
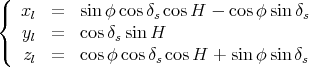 |
(24) |
et donc en combinant les équations (13) et (24) on obtient finalement :
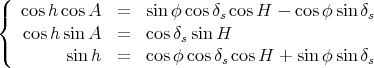 |
(25) |
À midi vrai (H = 0, A = 0), on obtient
 |
(26) |
Pour l’angle horaire du soleil H (heure solaire vraie), la longueur L′ = OC de l’ombre au le sol d’un style vertical de longueur L = OB vérifie la relation (figure 4) :
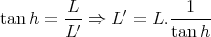 |
(27) |

|
L’angle A que fait l’ombre avec le méridien local (l’azimut, donc) vérifie (facilement obtenu à partir de l’équation (25))
 |
(28) |
Cet angle dépend de H et φ bien sûr, mais également de δs.
La longueur L′p de la projection de l’ombre du style sur le méridien local vaut
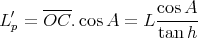 |
(29) |
Or lorsque δs = 0 (équinoxes de printemps et d’automne), on a (d’après (25))
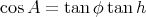 |
(30) |
donc dans ce cas particulier, la longueur de la projection est une constante :
 |
(31) |
L’extrêmité de l’ombre parcourt donc une droite perpendiculaire au méridien local.
On incline le style de manière à ce qu’il fasse un angle π∕2 - φ avec la verticale. Il est alors parallèle à l’axe de rotation de la Terre. On note Ls = OB′ la longueur du style incliné, définie par la relation
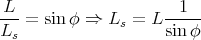 |
(32) |
Dans le triangle (OO′C′), on a 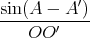 =
=  . Après un peu de calcul, on
trouve la relation
. Après un peu de calcul, on
trouve la relation
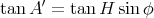 |
(33) |
Dans le cas du style incliné, l’angle que fait l’ombre avec le méridien local en fonction de H ne dépent plus de la déclinaison δs, d’où l’intérêt de cette géométrie pour la construction d’un cadran solaire. La longueur L′s = OC′ de l’ombre se calcule à l’aide du théorème de Pythagore :
 |
(34) |
Cette longueur peut également se calculer en utilisant la notation vectorielle :
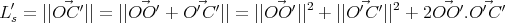 |
(35) |
On trouve finalement :
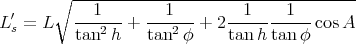 |
(36) |
À midi vrai, la relation (36) se simplifie et la longueur de l’ombre devient
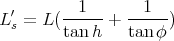 |
(37) |
En utilisant les relations (26) et (32), on peut encore simplifier pour obtenir une relation entre la longueur de l’ombre et la longueur du style incliné à midi vrai :
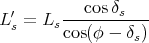 |
(38) |
Si l’on regarde la longueur L′sp de la projection de l’ombre sur le méridien local, on a cette fois
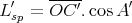 |
(39) |
Pour le cas particulier δs = 0, on obtient après un peu de calcul la relation
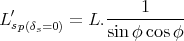 |
(40) |
L′sp(δs=0) est donc une constante et l’extrêmité de l’ombre parcourt une droite
perpendiculaire au méridien local. En fait cette propriété est évidente après le calcul du
style droit et l’étude attentive de la figure 4, la valeur de la projection pouvant être
calculée également très facilement si l’on appelle 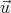 le vecteur unitaire porté par le
méridien local :
le vecteur unitaire porté par le
méridien local :
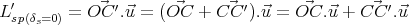 |
(41) |
or le calcul de 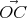 .
.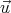 correspond à celui du style droit, et par construction
correspond à celui du style droit, et par construction 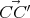 =
= 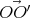 ,
on en déduit donc finalement
,
on en déduit donc finalement
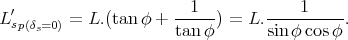 |
(42) |
On peut constater avec soulagement que l’équation (42) est identique à (40) et est bien compatible avec l’équation (38).
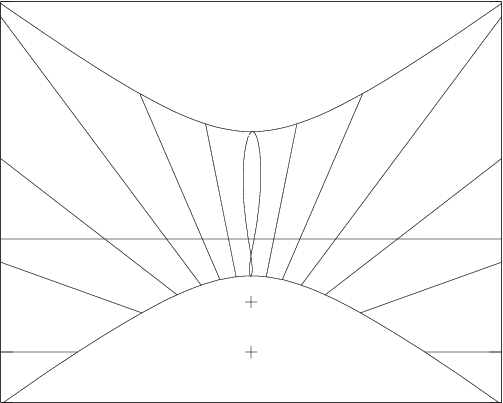
Avec les formules qui précèdent, on est en mesure de dessiner un cadran solaire. Le cadran représenté sur la figure 5 a été calculé pour une latitude de 48, 3∘ Nord.
|
La courbe en huit visible sur la ligne du midi vrai est parfois appelée analemme. Elle est la conséquence de l’équation du temps. Les lignes de déclinaison pour les solstices et les équinoxes sont également visibles. La lecture de l’heure sur un cadran solaire sera explicitée dans la section 4.
Le soleil se lève et se couche lorsque h = 0. Des équations (25) on déduit qu’à ce moment là, H doit vérifier la relation
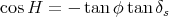 |
(43) |
On montre qu’alors
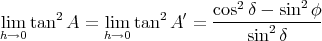 |
(44) |
Il est possible de calculer l’azimuth du Soleil au moment de son lever et de son coucher. À partir de la première ligne de l’équation (25), en posant h = 0 et en substituant H à l’aide de la formule (43), on obtient
 |
(45) |
Lorsque la déclinaison est positive, A est supérieur à π∕2, le Soleil se lève «avant» l’Est, et se couche «après» l’Ouest. Les jours d’équinoxe, il se lève exactement à l’Est et se couche exactement à l’Ouest.
On peut également déterminer l’angle θs que fait le Soleil avec l’horizon au lever et au coucher. Pour cela, on dérive l’équation (25) par rapport à H et à l’aide de l’équation (43) on trouve finalement
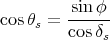 |
(46) |
Il est cependant possible que le soleil ne se lève jamais ou ne se couche jamais. En effet, sinh > 0 implique par exemple φ > π∕2 -δ. Au Pôle Nord (φ = π∕2), cette relation est vérifiée dès que δ > 0, c’est-à-dire de l’équinoxe de printemps à l’équinoxe d’automne. De manière plus générale, pour des latitudes supérieures à 66∘ ou inférieure à -66∘, il existe un ou plusieurs jours ou le soleil ne se lève pas et ou le soleil ne se couche pas (plus on se rapproche des pôles, plus cette durée est longue).
Lors du jour le plus court (solstice d’hiver dans l’hémisphère nord), le soleil se lève-t-il également le plus tard et se couche-t-il le plus tôt ? À cause de l’équation du temps, la réponse est non [4]. Si l’on fait abstraction de cette équation, c’est bien lorsque le soleil se lève le plus tard et qu’il se couche le plus tôt que le jour est le plus court (les heures de lever et coucher sont symétriques par rapport au midi vrai d’après l’équation (43)). Mais en incluant l’équation du temps, l’heure légale se trouve décalée de sorte que le lever le plus tardif a lieu plus tard par rapport au solstice, alors que le coucher le plus tôt a lieu en avance par rapport au solstice. Sur la figure 6 sont représentées la durée du jour ainsi que les heures de lever et de coucher du soleil. Le jour le plus court est le 21 décembre. Le soleil se couche le plus tôt le 11 décembre, et il se lève le plus tard le 31 décembre. Ces calculs ont été effectués pour une latitude de 48.3∘. Pour une latitude plus faible, l’effet est encore plus marqué.

|
À un jour donné de l’année correspond une valeur δs de la déclinaison. Pour une valeur de la déclinaison, l’extrêmité de l’ombre du style suit une trajectoire bien précise. On a déjà vu précédemment que dans le cas particulier des équinoxes (δs = 0), cette trajectoire était une droite.
On va noter 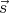 le vecteur unitaire indiquant la position du soleil, en choisissant
comme axe
le vecteur unitaire indiquant la position du soleil, en choisissant
comme axe 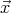 le méridien local et comme sens positif la direction vers laquelle pointe le
style, donc le Nord. D’après l’équation (25) on a
le méridien local et comme sens positif la direction vers laquelle pointe le
style, donc le Nord. D’après l’équation (25) on a
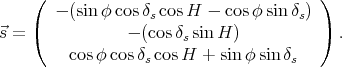 |
(47) |
Le vecteur 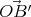 représentant le style s’écrit quant à lui
représentant le style s’écrit quant à lui
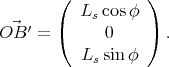 |
(48) |
Le produit scalaire de ces deux vecteurs donne
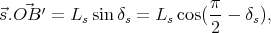 |
(49) |
il s’agit donc d’une constante (pour un jour donné) ! De cette dernière relation, on peut conclure que pour une déclinaison fixée, la trajectoire du soleil défini un cône de révolution dont l’axe est le style incliné (en réalité, il s’agit plutôt de l’axe de rotation de la Terre, mais vu du soleil, c’est pareil), dont le sommet est l’extrêmité du style, et dont le demi-angle d’ouverture au sommet vaut π∕2 - δs.
Les lignes de déclinaison vont ainsi être définie comme l’intersection du cône précedemment défini et du plan horizontal du cadran solaire. D’un point de vue purement mathématique, cette intersection peut être un cercle, une ellipse, une parabole ou une hyperbole.
Par construction, si l’on considère un point M de la ligne de déclinaison (ses
coordonnées sont (x,y, 0)), alors  et
et  sont colinéaires (M est la projection de B′
dans le plan suivant la direction du soleil
sont colinéaires (M est la projection de B′
dans le plan suivant la direction du soleil  ). On en déduit donc
). On en déduit donc
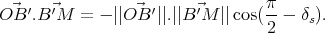 |
(50) |
Après élévation au carré, on trouve
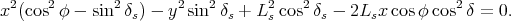 |
(51) |
Après mise en forme et en profitant du fait que cos 2φ- sin 2δ s = cos 2δ s - sin 2φ, on obtient finalement1
 |
(52) |
Pour des latitudes où le soleil se couche tous les jours de l’année, on a cos 2δ s - sin 2φ > 0, et on peut alors simplifier l’équation (52) en
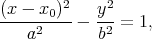 |
(53) |
avec
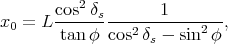 |
(54) |
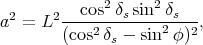 |
(55) |
et
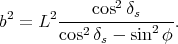 |
(56) |
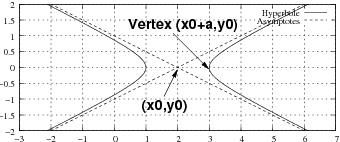
L’équation (53) représente une hyperbole (voir figure 7). Ses asymptotes sont
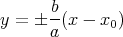 |
(57) |
et elles se croisent au point (x0, 0). On peut vérifier qu’on a bien
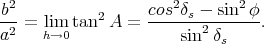 |
(58) |
Les points de coordonnées (x0 ± a, 0) (situés sur la courbe) sont nommés vertex.
Il est amusant de constater que x0 est la longeur moyenne de l’ombre à midi vrai pour les déclinaisons δs et -δs. En effet,
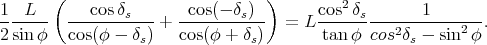 |
(59) |
|
On peut tracer les lignes de déclinaison grâce à la formule
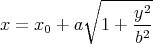 |
(60) |
Pour δs = 0, on obtient a = 0, et donc l’équation (60) se réduit à x = x0, ce qui est bien une droite. Par ailleurs on vérifie bien que x0 = L∕(sin φ cos φ), ce qui est conforme à l’équation (40).
Si l’on se trouve à une latitude où le soleil ne se couche pas un jour de déclinaison δs, alors cos 2δ s - sin 2φ < 0, et l’équation (52) est alors celle d’une ellipse :
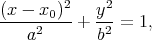 |
(61) |
avec
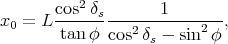 |
(62) |
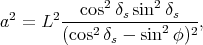 |
(63) |
et
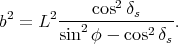 |
(64) |
La lecture de l’heure sur le cadran de la figure 5 se fait comme suit :
Donc en conclusion, le 20 novembre à Saint André Les Vergers, si le cadran solaire indique 12h, il est en réalité (12h + 1h - (16min20s) + (-15min)) = 12h28min40s.
Il est bien sûr possible de rajouter des lignes horaires pour les demi-heures, les quart-d’heure,...
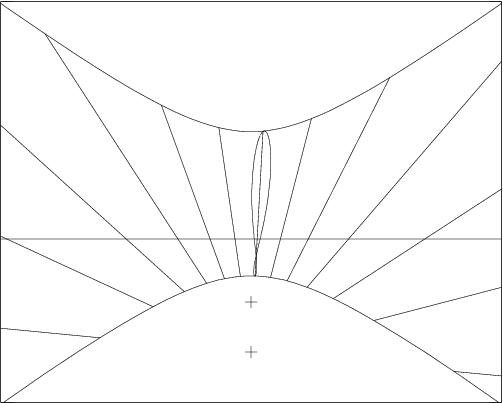
Une solution pour ne pas avoir à tenir compte de la longitude pour calculer l’heure légale est d’en tenir compte dans la construction du cadran. Ainsi sur la figure 8, les lignes horaires ont été décalées pour une longitude de 4∘4′ Est. La seule correction à faire après lecture provient donc de l’équation du temps (et bien sûr du décalage lié au fuseau horaire et éventuellement à l’heure d’été).
|
Pour s’affranchir également de cette correction, certains cadrans intègrent directement l’analemme, qui donne la valeur de l’équation du temps en fonction de la déclinaison. Généralement, seule la ligne horaire correspondant au midi vrai est agrémentée de cette courbe, mais il est possible de la tracer pour chaque ligne horaire. Ainsi le 20 novembre, lorsque l’ombre du style arrive sur le bord droit de l’analemme, il est très exactement 13h (le 21 janvier, date à laquelle la déclinaison est identique à celle du 20 novembre, c’est lorsque l’ombre du style arrive sur le bord gauche de l’analemme qu’ il est très exactement 13h).
Paradoxalement, la volonté de comprendre un peu mieux comment fonctionnaient les cadrans solaires m’est venue un soir où j’observais les étoiles à travers ce qui avait été le toit d’une partie de ma maison. Après de nombreuses soirées passées à trouver les formules utiles et à les programmer sont venues de nombreuses soirées pour redémontrer ces formules. Quelques souvenirs de mathématiques du lycée m’ont été utiles. Mais je me pose toujours une question : comment faisait-on autrefois sans calcul vectoriel et sans calculatrice ?
[1] http://www.astro.uu.nl/~strous/AA/en/reken/zonpositie.html.
[2] Site de l’Institut de Mécanique Céleste et de Calcul des Éphémérides. http://www.imcce.fr/fr/ephemerides/astronomie/Promenade/pages3/316.html.
[3] http://fred.elie.free.fr/cadrans_solaires.htm.
[4] http://members.aol.com/jwholtz/analemma/analemma.htm.
[5] http://www.astro.uu.nl/~strous/AA/en/reken/juliaansedag.html.
Pour le jour d du mois m de l’année j, on procède comme suit [5] :
Cette valeur est valable à minuit. Pour une heure quelconque h de la journée, il suffit d’ajouter h∕24 à d.
Soit M un point de coordonnées (x,y,z) dans le repère d’origine. Si le repère effectue
une rotation autour de l’axe 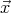 d’un angle θ, alors les nouvelles coordonnées de M sont
:
d’un angle θ, alors les nouvelles coordonnées de M sont
:
 |
(65) |
Si le repère effectue une rotation autour de l’axe 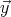 d’un angle θ, alors les nouvelles
coordonnées de M sont :
d’un angle θ, alors les nouvelles
coordonnées de M sont :
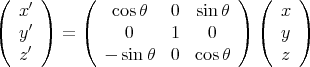 |
(66) |
Soit M un point de coordonnées sphériques (r,θ,φ), ses coordonnées cartésiennes sont :
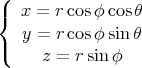 |
(67) |
 |
(68) |
 |
(69) |
 |
(70) |
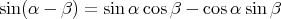 |
(71) |
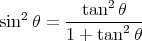 |
(72) |
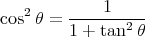 |
(73) |
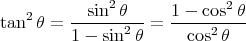 |
(74) |