) ;
Suite à la lecture de l’ouvrage « Devenez sorciers, devenez savants » de Georges Charpak et Henri Broch 1 , j’ai décidé de replonger dans mes cours de proba de Terminale C (déjà plus de vingt ans de cela). Dans un chapitre est en effet abordée la question de savoir s’il faut s’émerveiller ou pas du fait qu’un astrologue ait prédit 169 tremblements de terre pour les années 1994-1995-1996, et que 33 des dates données aient effectivement correspondu à des dates de séismes.
Les auteurs ont répertorié 196 dates de séismes pour les 1096 jours correspondants à ces trois années, et donnent comme probabilité d’avoir 33 dates communes 7, 1%, sans donner le détail du calcul. En faisant l’analogie avec mes vieux cours et les histoires de tirages de boules blanches ou rouges dans une urne, j’en suis arrivé à la conclusion qu’il me fallait calculer trois choses :
) ;
Cela donne pour finir p(33) = 
= 0, 0705, ce qui est bien le résultat attendu.
On peut refaire le calcul pour un nombre n de date correctes variant de 0 à 169, le calcul est
donc p(n) =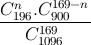 
, et l’on peut tracer le graphique (figure 2) présenté dans le livre.
On voit que la probabilité de prévoir moins de 12 dates correctes est négligeable, de même que la probabilité d’en prévoir plus de 50.
On peut reprendre le même genre de calcul, avec un jeu de 32 cartes. Si une persone choisit 8 cartes au
hasard, quelle est la probabilité qu’une autre personne en choisissant également 8 au hasard en
ait n en commun ? La réponse est p(n) = 
. Le résultat est présenté sur la figure 2.
On voit que la probabilité d’avoir 2 cartes communes dépasse les 35% ! Si on y ajoute la probabilité d’avoir 3 cartes communes, on arrive à 58, 5%. On peut donc proposer un petit jeu malhonnête à un ami, du genre « je parie que je devine 2 ou 3 cartes des 8 que tu choisis en en choisissant moi-même 8 ». Si chacun mise 1 €, l’espérance mathématique vaut 0, 585 × 1 - 0, 415 × 1 = 0, 17, c’est-à-dire qu’on gagne en moyenne 17 centimes à chaque partie.
