Multiplicateurs de Lagrange et calcul des variations : application au calcul de la distance d’un point à une droite dans le plan

Alexandre Vial

1er mars 2008

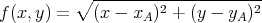
Résumé

Deux méthode de calcul de la distance entre un point et une droite sont présentées : la méthode des multiplicateurs de Lagrange, et le calcul des variations. Le but n’est pas de présenter la méthode la plus rapide ou la plus simple, mais de jouer avec ces deux méthodes.

1 Multiplicateurs de Lagrange

On cherche la distance entre un point A de coordonnées (xA,yA) et une droite (D) d’équation ax + by + c = 0. Par définition il s’agit donc de déterminer le minimum de la fonction

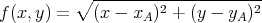∘ ---------2----------2- f (x,y) = (x - xA ) + (y - yA )
(1)

qui représente la longueur d’un segment de droite allant du point A à un point quelconque de la droite (D), avec par conséquent la contrainte

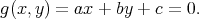g(x, y) = ax + by + c = 0.
(2)

On définit la fonction

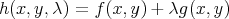h(x,y,λ) = f (x,y) + λg(x,y)
(3)

où λ est un multiplicateur de Lagrange (on définit autant de multiplicateurs qu’il y a de contraintes, donc un seul multiplicateur dans cet exemple), et on impose

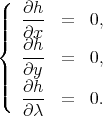( || ∂h- = 0, ||{ ∂x ∂h- = 0, || ∂y ||( ∂h- ∂λ = 0.
(4)

Par construction, la dernière équation est équivalente à la contrainte (2). Les deux premières équations conduisent à

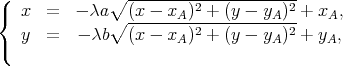( ∘ ---------------------- { x = - λa ∘ (x---xA)2-+-(y---yA)2-+ xA, y = - λb (x - xA)2 + (y - yA)2 + yA, (
(5)

et par insertion dans la troisième on obtient

λ = --------∘axA-+-byA-+--c---------. (a2 + b2) (x - xA)2 + (y - yA )2
(6)

Par réinjection dans (5) on obtient

( ||| x - xA = - aaxA--+-byA-+-c, { a2 + b2 y - y = - baxA-+--byA-+-c, |||( A a2 + b2
(7)

etc pour finir en utilisant (1) on trouve

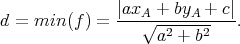|axA-+-byA-+--c| d = min (f) = √a2--+-b2 .
(8)

2 Calcul des variations

Dans la partie précédente, on a utilisé le fait que la distance était donnée par le segment de droite le plus court. Le calcul des variations permet d’établir que la distance la plus courte est bien celle d’un segment de droite, avant d’obtenir sa longeur.

On cherche à minimiser la longueur s définie par

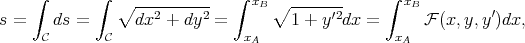∫ ∫ ∘ ---------- ∫ xB ∘ ------- ∫ xB s = ds = dx2 + dy2 = 1 + y′2dx = F (x,y,y′)dx, C C xA xA
(9)

où la borne supérieure d’intégration xB n’est pas fixée mais vérifie la relation

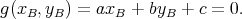g(xB,yB ) = axB + byB + c = 0.
(10)

s sera extrémale si F vérifie l’équation d’Euler-Lagrange [1] :

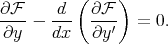( ) ∂F-- d-- ∂F-- ∂y - dx ∂y′ = 0.
(11)

Si de plus F ne dépend pas explicitement de x (ce qui est le cas ici), on peut alors utiliser l’identité de Beltrami :

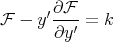′∂F-- F - y ∂y ′ = k
(12)

où k est une constante à déterminer à partir des conditions initiales.

Comme la seconde extrémité est libre, on doit aussi vérifier

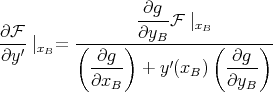∂g ∂F ∂y--F |xB --′-|xB = (-----)---B------(-----)- ∂y -∂g- + y′(x ) -∂g- ∂xB B ∂yB
(13)

Nous avons

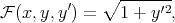∘ ------- F (x,y,y′) = 1 + y′2,
(14)

donc nous pouvons utiliser (12), qui donne

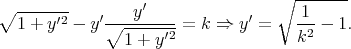′ ∘ ------- ∘1--+-y′2 - y′∘--y---- = k ⇒ y′ = -1-- 1. 1 + y′2 k2
(15)

Par conséquent, y′ est une constante, donc la courbe dont nous cherchons la longeur est un segment de droite.

Par ailleurs, d’après (13), on doit également avoir

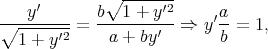∘ ------- y′ b 1 + y ′2 a ∘-------- = --------′- ⇒ y′--= 1, 1 + y ′2 a + by b
(16)

les dérivées y′étant calculées pour x = xB. Ce résultat montre que la droite cherchée est perpendiculaire à (D) (le produit de leurs pentes respectives, à savoir y′ et -a∕b, vaut -1).

Nous savons donc que la droite cherchée a pour pente b∕a et passe par le point (xA,yA), son équation est donc

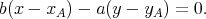b(x - xA) - a(y - yA) = 0.
(17)

La borne supérieure d’intégration xB est déterminée par l’intersection des droites décrites par (10) et (17), et on trouve

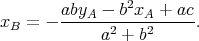2 x = - abyA---b-xA-+-ac-. B a2 + b2
(18)

La distance cherchée s’obtient en calculant

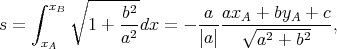∫ ∘ ------- xB b2- a--axA-+-byA-+-c- s = 1 + a2dx = - |a | √a2--+-b2 , xA
(19)

elle peut être négative ou positive, il s’agira donc d’un maximum ou d’un minimum (on rappelle que le calcul des variations fournit un extremum), on s’affranchit du problème en prenant la valeur absolue (une distance est positive), et on retrouve bien le résultat (8).

Références

[1]   Robert Weinstock: Calculus of variations, chapitre 3. Dover publications, Inc., New York, 1974.