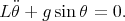
On considère un pendule simple, mais on remplace le fil par un ressort. Pour le pendule simple, on a
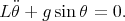 | (1) |
En coordonnées polaires, l’accélération s’écrit
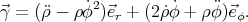 | (2) |
Les projections suivant 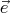 ρ et
ρ et 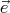 φ donnent
φ donnent
 | (3) |
On introduit les variables φ1 = φ, φ2 = 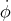 =
= 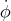 1, ρ1 = ρ et ρ2 =
1, ρ1 = ρ et ρ2 =  =
= 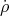 1, et on peut alors écrire le
système (3) sous la forme
1, et on peut alors écrire le
système (3) sous la forme
 | (4) |
Pour limiter l’élongation du ressort, il est judicieux d’utiliser comme force de rappel quelquechose du genre
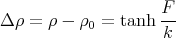 | (5) |
soit
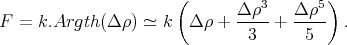 | (6) |
Exemple : ω0 = 2π, ρ0 = 1.