Le glaçon et l’igloo

Alexandre Vial

24 décembre 2007

Résumé

Un glaçon glisse sans frottements sur la surface d’un igloo. À partir de quel moment le glaçon n’est-il plus en contact avec la surface ? On cherche la réponse pour un igloo sphérique, puis cycloïdal.

1 Igloo sphérique

Un considère un igloo de forme sphérique, la trajectoire du glaçon au contact est donc un cercle de rayon R (figure 1).

FIG. 1:

Igloo sphérique.

La hauteur du glaçon vaut

h = R sin θ.

(1)

On considère que le glaçon glisse sans frottement à partir du sommet de l’igloo avec une vitesse initiale nulle. Par conséquent, en utilisant le fait que ΔE_c = -ΔE_p, on peut calculer la vitesse en fonction de θ :

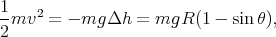1- 2 2mv = - mg Δh = mgR (1 - sin θ),

(2)

et donc

v2- R = 2g (1 - sinθ ).

(3)

On applique ensuite la relation fondamentale de la dynamique ∑ _ext = m, les forces qui s’exercent sur le glaçon sont le poids ⃗
P dirigé vers le bas et la réaction normale ⃗
R _N, et on s’intéresse plus particulièrement à la composante normale de l’accélération, ce qui donne

v2- - m R = - mg sin θ + RN ,

(4)

et en utilisant le résultat donné par l’équation (3), on peut exprimer la réaction de l’igloo sur le glaçon comme

R = mg (3 sin θ - 2). N

(5)

Cette réaction s’annule (et donc le glaçon n’est plus au contact de la surface de l’igloo) pour

2- ∘ sin θ0 = 3 ⇒ θ = 41,81 ,

(6)

ce qui correspond à une hauteur

h = 2R- = 2hmax- 3 3

(7)

et à une vitesse

∘ ----- 2Rg- vmax- v = 3 = √3--.

(8)

2 Igloo cycloïdal

La trajectoire du glaçon au contact est cette fois une arche de cycloïde dont le cercle générateur a pour rayon R, l’altitude peut être exprimée comme

z = R(1 - cos(t + π)) = 2R sin2 t +-π 2

(9)

où 0 < t < π représente l’angle dont a tourné le cercle générateur (voir figure 2), et en considérant toujours que le glaçon glisse sans frottement depuis le sommet,

1mv2 = - mg Δh = 2Rmg (1 - sin2 t-+-π ) = 2Rmg cos2 t-+-π, 2 2 2

(10)

donc la vitesse vaut

t + π v2 = 4Rg cos2 -----. 2

(11)

FIG. 2:

Igloo cycloïdal.

Par ailleurs, on sait que la tangeante à la trajectoire est définie par

∘ -------- dz 2R - z --- = ± -------, dx z

(12)

donc la normale à la trajectoire sur la partie descendante est définie par

∘ ---z---- ∘ -z-- t + π tan θ = ------- ⇒ sin θ = ---= sin -----. 2R - z 2R 2

(13)

Une autre possibilité pour obtrenir ce résultat est de se souvenir que pour la cycloïde, NM est perpendiculaire à la vitesse, elle-même tangeante à la trajectoire, donc NM est normal à la trajectoire (M est le point de la cycloïde et N le point de contact du cercle générateur sur l’horizontale). NQ est un diamètre du cercle (passant donc par son centre O), le triangle NOM est isocèle, donc par construction 2(π∕2 - θ) + (π - t) = π, donc θ = π---t
2 , et sin θ = sin = sin π +-t
2 .