Dans un premier article, j’ai présenté l’étude du cadran à chapeau dans le cas où le chapeau circulaire recouvre un cylindre. Dans le présent article, je montre comment il est possible d’utiliser un tronc cônique.

1 Limite ombre-lumière

Contrairement au cas du cylindre, les deux limites ombre-lumière pour un cône ne sont pas dans le plan vertical passant par l’axe du cône et dont la normale est donnée par l’azimut du Soleil. Ce qui veut dire que le cône n’est pas assimilable à une superposition de cylindres. Pour s’en convaincre, il suffit de regarder les figures 1(a) et 1(b), calculées pour la même position du Soleil. Alors que sur la première, on voit nettement la limite, sur le seconde, elle n’est pas visible.

(a) Superposition de cylindres.

(b) Cône.

FIGURE 1: Limite ombre-lumière.

Sur la figure 2, on voit nettement que les limites ombre-lumière ne sont pas dans un plan passant par l’axe du cône.

FIGURE 2: Limite ombre-lumière pour un cône.

Comment calcule-t-on la position de cette limite sur un cône ?

Soit le vecteur normal au cône, et le vecteur donnant la position du Soleil, on trouve la limite ombre-lumière lorsque . 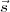= 0. En notant A l’azimut du Soleil mesuré depuis le Sud , h la hauteur du Soleil, θ l’angle polaire d’un point sur le cône (également mesuré depuis le Sud), et α le demi-angle d’ouverture au sommet du cône, on a

(1)

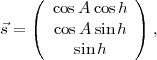(2)

par conséquent le calcul de . = 0 conduit à

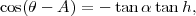(3)

et donc

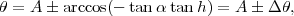(4)

avec

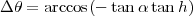(5)

(voir la figure 3).

FIGURE 3: Représentation de quelques angles.

Il y a donc une limite ombre-lumière seulement si tanα tanh < 1, c’est-à-dire si α < π∕2 -h. Pour avoir une limite tout au long de l’année, on doit donc avoir α < π∕2 -h_Max, avec h_Max = π∕2 -ϕ + ϵ, ϕ la latitude du lieu et ϵ l’obliquité de l’axe de rotation de la Terre (pour une déclinaison δ du Soleil, sa hauteur maximale vaut π∕2 - ϕ + δ ). La condition sur l’existence de la limite s’exprime donc comme

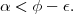(6)

L’équation (5) exprime le fait qu’en fonction de la hauteur du Soleil, Δθ va varier, et donc contrairement au cas du tronc cylindrique (pour lequel Δθ = π∕2), la ligne du midi vrai ne sera pas une ligne verticale, mais une ligne courbe.

2 Lignes horaires

2.1 Calcul des lignes

Le cadran est schématisé sur la figure 4.

FIGURE 4: Schéma du cadran.

Le calcul des lignes horaires se fait en cherchant l’intersection de l’ombre du chapeau (disque de rayon R) avec une des deux lignes délimitant les zones claires et sombres. Pour cela, on prend un point quelconque A du bord du chapeau, de coordonnées (x_A,y_A,0). On calcule sa projection parallèlement au vecteur 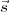dans le plan (P) passant par l’axe du cylindre et la limite de droite par exemple (lorsque l’on a le Soleil dans le dos en regardant le cylindre).

Pour se simplifier la vie, on se place dans un référentiel tel que 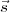n’a qu’une composante horizontale non-nulle (figure 3). Ainsi

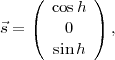(7)

et le plan (P) est défini par son vecteur normal

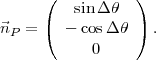(8)

On trouve alors que le projetté A′ de A dans le plan (P) a pour coordonnées

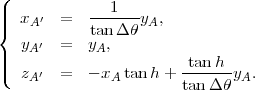(9)

De plus, A′étant sur la droite limite sur le cône, ses coordonnées doivent vérifier l’équation supplémentaire

(10)

avec p = et q = -r_Hp, r_H étant le rayon supérieur du cône (voir figure 4).

En combinant la dernière ligne de (9) avec (10), on obtient l’équation suivante à résoudre :

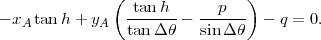(11)

On pose alors x_A = R cosθ, y_A = R sinθ, puis t = tan, sinθ = , cosθ = 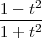, et le problème se ramène au calcul des racines d’une équation du second degré :

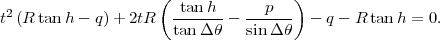(12)

En écrivant de manière plus compacte (12) sous la forme at² + 2bt + c = 0, la solution qui nous intéresse est t = 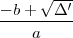avec Δ′ = b² -ac. On peut alors remonter à θ, puis à x_A et y_A, puis aux coordonnées de A′.

2.2 Tracé des lignes

Pour tracer les lignes horaires, on va « dérouler le cône » (figure 5) et travailler en coordonnées polaires (r,θ). On calcule tout d’abord la longeur de l’ombre depuis le point fictif O′ :

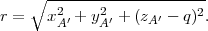(13)

FIGURE 5: Cône déroulé pour le tracé des lignes horaires.

Pour l’angle, on effectue une mise à l’échelle et un décalage : en effet la longeur du cercle supérieur vaut 2πr_H, mais vaut également r_H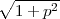.2θ_Max (depuis O′, le rayon du cercle est r_min = 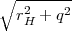= r_H), de plus Δθ est toujours supérieur ou égal à π∕2, on peut donc retrancher cette valeur afin de center le dessin autour de 0, d’où finalement

(14)

(on a rajouté un signe -à l’azimut à cause de la convention de signe pour ce dernier, qui comme les angles horaires, est compté positif dans le sens anti-trigonométrique). On calcule r_max à partir de la longueur r de l’ombre le jour du solstice d’été à midi vrai.

On peut à présent tracer les lignes horaires. Un exemple est présenté sur la figure 6 pour ϕ = 48,3∘, avec R = 1, r_H = 0,5 et α = 15∘ (les heures de l’après-midi sont dans la partie « basse » du dessin). On peut constater que la ligne de midi vraie n’est pas une ligne verticale, contrairement au cas du tronc cylindrique.

FIGURE 6: Exemple de tracé de lignes horaires pour une latitude ϕ = 48,3∘, chapeau sur la gauche.

Le résultat final est visible sur la figure 7.

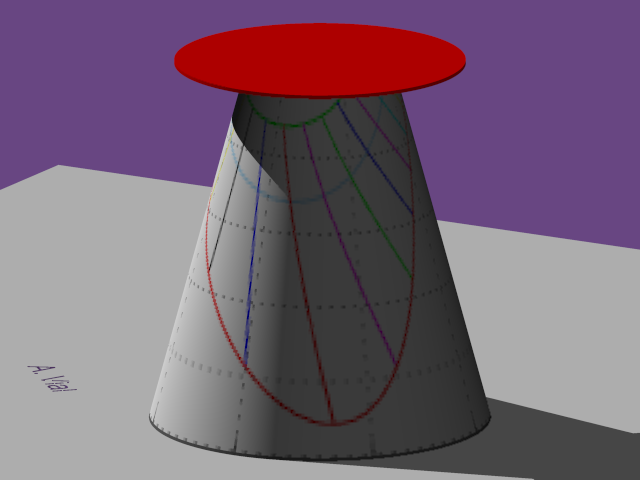
(a) Le 21 mars à midi solaire.

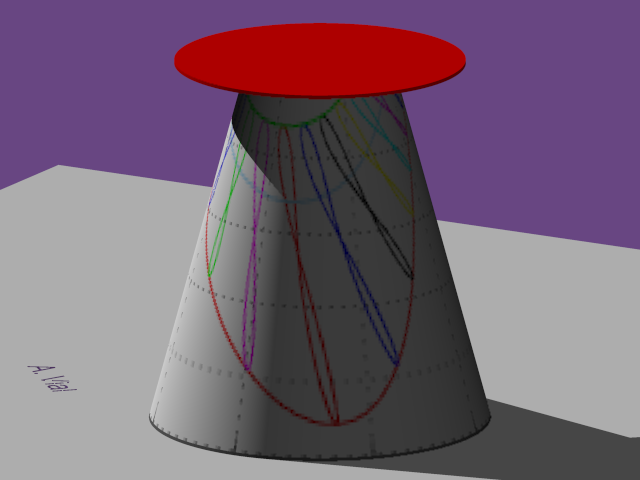
(b) Le 21 mars à midi moyen.

FIGURE 7: Cadran final, sans et avec analemme.

Afin de rendre ce cadran plus « amusant », il est possible de changer la forme du chapeau (à condition de garder une base circulaire), comme on peut le voir figure 8, avec le cadran « champignon ».

FIGURE 8: Cadran « champignon », le 21 mars à midi solaire.