FIGURE 1: Schéma du bol retourné.
Résumé
Quelle hauteur d’eau permet de soulever un bol hémisphérique à l’envers ?
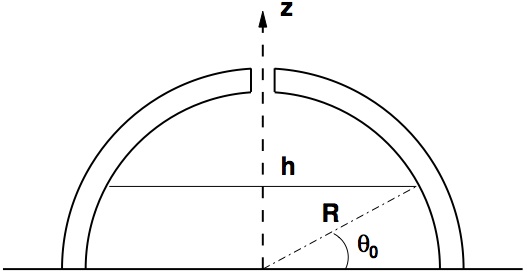
On considère un bol de forme hémisphérique, de rayon R, d’épaisseur e << R, de masse volumique ρbol posé à l’envers. Il contient un liquide de masse volumique ρ, dont la hauteur h peut-être modifiée grâce à un trou sur le sommet du bol.
On note z = R sin θ et h = R sin θ0.
La pression à une hauteur z vaut
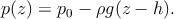 | (1) |
Pour calculer la force élémentaire qu’exerce le liquide sur un élément de surface d
tel que
 | (2) |
il suffit de calculer
 | (3) |
p0 contribue à la force exercée sur le bol à l’intérieur et à l’extérieur, donc les deux contributions vont se compenser, la force totale résultante n’en dépend pas, et par symétrie, cette force sera orientée verticalement, vers le haut (c’est donc la projection de la force élémentaire sur l’axe vertical qui est utile, ce qui fait apparaitre un terme sin θ supplémentaire) :
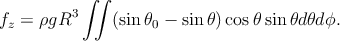 | (4) |
On obtient donc
Simple non ?Le bol se soulève si la force calculée précédemment est supérieure au poids du bol : fz ≥ Pbol. Or
 | (9) |
Ce qui conduit à
 | (10) |
ou encore
 | (11) |
![∫ θ0
fz = 2πR3 ρg (sin θ0sinθ cosθ - sin2θ cosθ)dθ (5)
0
( [ 2 ]θ0 [ 3 ] θ0)
= 2πR3 ρg sin θ0 sin--θ- - sin-θ- (6)
2 0 3 0
= 1-πρgR3 sin3θ0 (7)
3
1- 3
= 3 πρgh . (8)](bol5x.png)